UFJF, Sem Campus, Física 1, AV1 - 2016.1, Questão 1a
[1] Uma bola de beisebol é golpeada a uma altura e apanhada na mesma altura, conforme a figura. Deslocando-se paralelamente a um muro, ela passa pelo alto do muro após ter sido golpeada e, novamente, depois quando está descendo, em posições separadas por uma distância
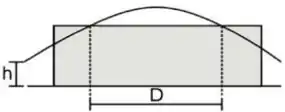
(a) Escolha um sistema de coordenadas e escreva o vetor velocidade inicial da bola imediatamente após ela ter sido golpeada. Qual o ângulo que faz com a horizontal?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema temos uma bola que é lançada com velocidade que possui um ângulo com a horizontal. Após a bola passa pelo alto de um muro e depois de passa pelo alto do muro novamente. Nesse intervalo a bola se desloca uma distância horizontal .
Com isso, queremos descobrir o vetor velocidade inicial e o ângulo que ele faz com a horizontal.
Tem ideia de como fazemos isso? 😁
Esse lançamento possui uma característica universal... em lançamentos balísticos o movimento horizontal é constante e o movimento vertical é acelerado devido a ação da força gravitacional.
Vamos usar essa informação a nosso favor! 😎
Passo 2
Horizontalmente a bola de desloca em um intervalo de tempo de pelo que vimos no intervalo de tempo em que a bola passa pelo topo do muro.
Assim, a velocidade horizontal pode ser calculada como
Agora vamos calcular a velocidade inicial vertical da bola.
Pra isso, podemos calcular a velocidade vertical no instante em que a bola passa pelo alto do muro pela primeira vez e depois obter a velocidade inicial sabendo que a bolinha demorou para atingir esse ponto.
Aplicando a fórmula
Com , e , temos
Tranquilo até aqui? 😬
Passo 3
Agora, sabendo que a bola demorou para atingir esse ponto, temos
Portanto o vetor velocidade inicial é dado por
Já para encontrar o ângulo desse vetor com a horizontal, calculamos
Fim! Iae, o que achou? Responde Aí! 😁
