UFMG – Fundamentos de Mecânica – P1 – Questão P1.2
Um cineasta filma a erupção de um vulcão e, num certo instante, ele registra um bloco sendo arremessado fazendo um ângulo com a horizontal, partindo da boca do vulcão de uma altura a partir do solo. Ele acompanha o movimento do bloco e o filma batendo no solo, como na figura, um tempo após ser lançado. Desprezando a resistência do ar,
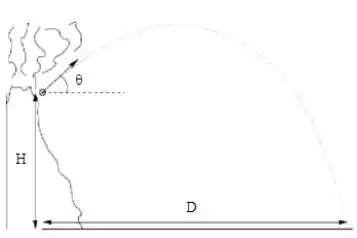
- Calcule a distância horizontal que o bloco percorreu do instante em que foi arremessado da boca do vulcão até o momento que se chocou com o solo, em função de e .
Passo 1
Oi, tudo bem?
Esse corpo leva um tempo para atingir o chão, ou seja, durante esse tempo é que ela atinge o maior alcance horizontal, então é essa a informação chave que vamos usar!
Relembrando das equações de movimento para a componente (isso porque queremos saber , que está na direção horizontal)
E ideia para resolver questões de cinemática é comparar os dados que temos com as equações! Nesse caso só temos uma equação, pois em relação ao movimento horizontal, a bolinha apresenta um MRU!
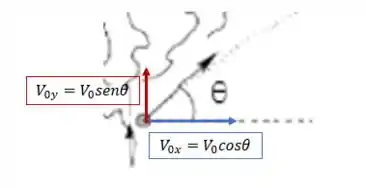Isso sem esquecer que a velocidade inicial pode ser decomposta em componente vertical e horizontal:
Vemos que a componente vertical aponta para cima! Então a velocidade inicial em é positiva! Já a componente horizontal aponta para a direita, e assumimos que esse é o sentido positivo.
tranquilo até aqui? Vamos começar?
Passo 2
Do passo anterior temos a velocidade inicial (na direção de ) que a bolinha tem:
E ele mantém essa velocidade durante toda trajetória, já que na horizontal não há aceleração! Então a distância que o bloco percorre horizontalmente é proporcional ao tempo transcorrido e a velocidade!
No item anterior dessa questão foi pedido para calcular o módulo da velocidade inicial do bloco :
Essa velocidade foi determinada a partir da equação horária do movimento em , usando a condição inicial de que e , que o bloco leva um tempo para atingir o chão e jogamos tudo isso na equação .
A ideia agora é relacionar essa velocidade com a equação do MRU para a distância percorrida
Passo 3
A distância percorrida , quando a bolinha tem uma velocidade durante o tempo é dada pela única equação do MRU:
Não queremos saber as posições, mas sim o alcance, então ! Agora substituindo a velocidade e o tempo temos :
Agora substituindo a velocidade inicial
Temos o valor de :
Podemos simplificar e transformar , aí teremos a resposta mais simplificada:
E é isso!
Espero ter ajudado!