Um navio de guerra atira simultaneamente dois mísseis em navios inimigos. Se os mísseis seguem as trajetórias parabólicas mostradas, qual das afirmações é correta:
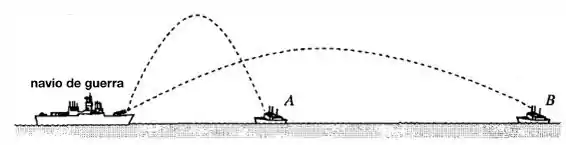
(a) Só é possível determinar a ordem de chegada dos mísseis conhecendo-se o valor exato dos ângulos de lançamento.
(b) O navio B é atingido primeiro.
(c) Só é possível determinar a ordem de chegada dos mísseis conhecendo-se as magnitudes das velocidades de lançamento.
(d) O navio A é atingido primeiro.
(e) Os navios A e B são atingidos simultaneamente.
Passo 1
Ele tá pedindo pra gente ver qual o míssil chega primeiro no seu destino, e se é possível determinar isso.
Bom, estamos falando de um lançamento oblíquo.
Então algumas observações:
No eixo x temos um movimento uniforme, porque não temos aceleração.
No eixo y temos um movimento uniformemente variado, porque temos aceleração da gravidade apontando pra baixo.
Portanto para cada eixo, vamos usar as equações de movimento adequadas, tipo, no eixo x são as equações de MU, e no eixo y são as equações de MUV.
O tempo que a partícula leva pra ir da origem até ponto final da trajetória é o dobro do tempo que ela leva pra ir da origem até o ponto mais alto.
Na altura mais alta, a velocidade no eixo y é zero, porque a partícula já subiu tudo o que ela conseguia subir, então agora ela para e começa a descer. Olha lá pra nossa figura com os vetores velocidade em y e a aceleração da gravidade apontando pra baixo
Beleza, esses foram só uns lembretes de movimento obliquo.
Vamos ver se a gente consegue descobrir qual míssil chega no seu destino primeiro.
Acompanha comigo.
Passo 2
A gente viu que no eixo y é um MUV, por causa da aceleração da gravidade. Então vamos escrever as equaçãos para a posição e velocidades do eixo y:
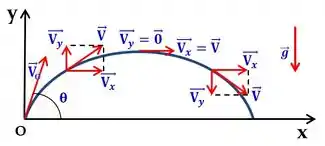
A gravidade tá apontando pra baixo em relação ao eixo y, então ficamos com .
Beleza?
Agora, vamos ver o tempo de subida , que é metade do tempo que o míssil leva pra fazer toda a trajetória:
No ponto mais alto , então:
O tempo de subida é igual ao tempo de descida , então o tempo total é:
Beleza, já temos uma equação que fala sobre o tempo que o míssil demora pra chegar no destino. Mas não temos informação da velocidade inicial. E aí? Morremos na praia?
Não!!!
Olha lá pra figura, temos ainda outra informação. A altura máxima do A, é maior do que a altura máxima do B, . Então vamos a equação de posição do eixo vertical:
O é zero,porque colocamos a origem ali no ponto de lançamento dos mísseis. E o tempo que demora pra chegar até é o . Então:
Substituindo :
Ajeitando isso daí:
Maravilha! Substituindo a velocidade naquela equação para o tempo total de percurso:
Passo 3
Usando essa relação e a informação da figura que :
Como o tempo total é proporcional a raiz da altura, e como a altura de A é maior do que a altura do B, então o tempo total de A também é maior do que o tempo total de B
Então o míssil cai primeiro em B.
Resposta
Alternativa B