Lançamento Oblíquo
Dois canhões apontam-se mutuamente, como mostrado na figura, e disparam suas balas no mesmo instante de tempo. O canhão dispara sua bala com velocidade de módulo , e o canhão com velocidade . As distâncias no problema são .
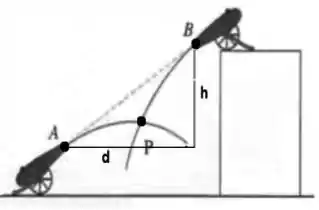
a) Qual a aceleração de cada uma das balas após o disparo?
b) Quanto tempo se passou a partir do momento do disparo até o instante da colisão? A que altura acontece a colisão?
c) Se não houvesse o canhão , qual seria o alcance da bala do canhão A?
Passo 1
a)
As balas realizam lançamentos oblíquos. Estão sujeitas apenas a aceleração da gravidade, ou seja,
Passo 2
b)
Com a origem no ponto e o ângulo entre a inclinação do canhão e a horizontal, pelas fórmulas do lançamento oblíquo de alcance e do eixo , temos:
Logo quando acontece a colisão temos que , assim obtemos que:
Fazendo :
Portanto:
Ou seja, a colisão acontece a de altura.
Passo 3
c)
Como já que o triângulo na figura é isóscele, temos o alcance máximo:
Resposta
a)
b) ;
c)