(inspirada no 2° testinho) Uma partícula é lançada do solo com velocidade de módulo , fazendo um ângulo com a horizontal, tal que e . Após , a partícula colide com o ponto A da figura abaixo. Despreze a resistência do ar e
considere .
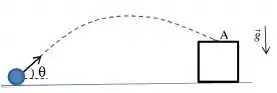
(a) Qual é a altura do ponto A em relação ao ponto de partida?
(b) Determine o vetor velocidade da partícula imediatamente antes da colisão com o ponto
A.
Passo 1
Temos um lançamento oblíquo, de inclinação . No instante , a partícula chega no ponto A, onde ela colide.
Queremos saber a altura do ponto A e também a velocidade da partícula logo antes da colisão.
Passo 2
(a) Qual é a altura do ponto A em relação ao ponto de partida?
Vamos analisar separadamente o movimento vertical e horizontal.
Para isso, vamos achar as componentes da velocidade inicial .
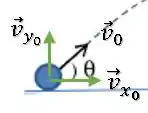
Temos que os módulos das velocidades e no instante inicial são:
Para achar a altura , vamos olhar primeiro o movimento vertical, que é um movimento uniformemente variado:
A posição inicial é zero, a velocidade inicial é e a aceleração da gravidade é no sentido contrário da velocidade:
Se a partícula leva para chegar em A, basta nós substituirmos :
Temos que , e :
Então, achamos que a altura do ponto A é .
Passo 3
(b) Determine o vetor velocidade da partícula imediatamente antes da colisão com o ponto
A.
Estamos trabalhando com as componentes e da velocidade.
Para achar a velocidade no ponto A, basta calcularmos cada uma dessas componentes.
Componente em :
Na horizontal, a partícula realiza um movimento uniforme, logo, sua velocidade em todo o trajeto será igual à sua velocidade inicial :
Componente em :
Podemos calcular sua velocidade vertical em A com:
A velocidade inicial é:
Sendo que no ponto A, o instante é , logo:
Já que achamos uma velocidade negativa, significa que essa componente aponta para baixo.
Então, é só juntarmos as duas componentes e temos a velocidade :
Resposta
(a)
(b)