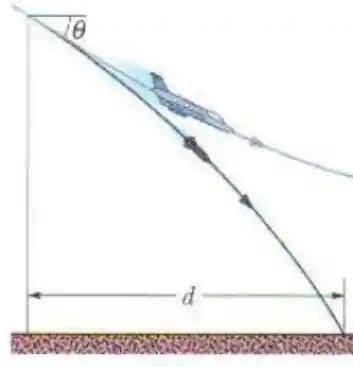
Um certo avião tem uma velocidade de e está mergulhando com um ângulo abaixo da horizontal quando o piloto libera um chamariz. A distância horizontal entre o ponto de lançamento e o ponto onde o chamariz se choca com o solo é . Quanto tempo o chamariz passou no ar? De que altura foi lançado?
Passo 1
É um problema de lançamento oblíquo, onde a questão nos deu o alcance, a velocidade inicial e o ângulo q a velocidade faz com o eixo .
Porém é um exercício um pouco diferente do comum, pois o ângulo dado está abaixo do eixo e o lançamento não é para cima. Mas, pode ficar tranquilo a resolução é igual.
Passo 2
Queremos saber quanto tempo que o chamariz passou no ar, ou seja, o tempo que ele gastou para percorrer no eixo .
Por isso, pela equação do movimento em
Vamos decompor a velocidade pela regra do “COlado/Separado”
Passando a velocidade em para , teremos:
Agora podemos substituir na equação da posição
Passo 3
Agora que temos o tempo de voo, precisamos apenas da equação da posição do movimento em
Precismos achar e para isso vamos usar a regra do “COlado/Separado”
Passando a velocidade para
Substituindo na equação
Observe que a velocidade é negativa pois o lançamento é para baixo, logo é negativa. Agora substituindo o tempo que encontramos temos