UFJF, Sem Campus, Física 1, AV1 - 2016.1, Questão 1c
[1] Uma bola de beisebol é golpeada a uma altura e apanhada na mesma altura, conforme a figura. Deslocando-se paralelamente a um muro, ela passa pelo alto do muro após ter sido golpeada e, novamente, depois quando está descendo, em posições separadas por uma distância
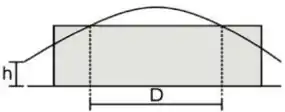
(c) Qual a distância horizontal percorrida pela bola do instante em que foi golpeada até ser apanhada?
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos uma bola que é lançada com velocidade que possui um ângulo com a horizontal. Após a bola passa pelo alto de um muro e depois de passa pelo alto do muro novamente. Nesse intervalo a bola se desloca uma distância horizontal .
Com isso, queremos descobrir qual é espaço horizontal total que a bola percorre.
Tem ideia de como fazemos isso? 😁
Anteriormente vimos que a velocidade inicial da bolinha é dada por
Assim, sabendo o tempo que a bolinha ficou no ar, podemos calcular o espaço que a bola percorreu.
Sacou? Bora começar! 😁
Passo 2
Sabemos que o tempo de subida é igual ao tempo de descida então se a bola leva para atingir o topo do muro e para atingir o mesmo ponto na descida, então a bola leva mais do topo do muro até ser pego.
Dessa forma, o tempo total do lançamento é dado por
Sabendo o tempo e a velocidade, podemos calcular o espaço horizontal como
O que achou? Foi de boa? Responde aí! 😊
