Uma bola de neve de é lançada de um penhasco de de altura. A velocidade inicial da bola de neve é de , acima da horizontal. Qual é o trabalho realizado sobre a bola de neve pela força gravitacional durante o percurso até um terreno plano, abaixo do penhasco? Qual é a variação da energia potencial do sistema bola-de-neve Terra durante o percurso? Se a energia potencial gravitacional é tomada como sendo nula na altura do penhasco, qual é o seu valor quando a bola de neve chega ao solo?
Passo 1
Oiie, tudo bem?
O enunciado descreve a situação de um lançamento oblíquo. Algum personagem desconhecido que está no topo de um penhasco à uma altura de lança uma bolinha de neve com massa obliquamente com um ângulo de com a horizontal, como o seguinte esquema
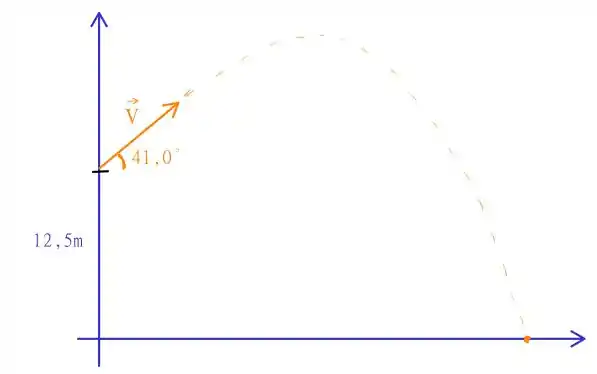
A alternativa nos pede para calcular o trabalho realizado pela força gravitacional para chegarmos até a base do penhasco após o lançamento oblíquo. Podemos fazer isso considerando o teorema de variação da energia cinética como
E, através deste resultado, temos que a alternativa é obtida diretamente através da expressão
Até aqui consideramos como referencial de potencial nulo a base do penhasco, em , agora no entanto, a alternativa pede com que mudemos o nosso referencial e tomemos como potencial nula a altura . Consegue imaginar que tipo de diferença isso irá causar nos valores? Vem comigo!
Passo 2
Temos que a velocidade tem uma componente em e outra em . A componente em é constante, já que a única força que atua neste sistema é a força gravitacional puxando a bolinha para baixo, sendo assim, não há variação da energia cinética na horizontal. A componente vertical, no entanto, varia e precisamos estimar esta variação se quisermos obter o trabalho realizado!

A componente vertical da velocidade pode ser obtida analisando o seguinte triângulo retângulo
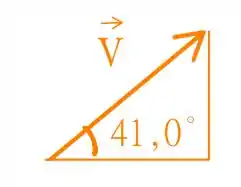
A hipotenusa deste triângulo é dada pelo módulo da velocidade inicial como , e portanto, a componente vertical pode ser obtida como
De forma que temos o seguinte valor para a componente vertical
Maravilha! Com isso temos meio caminho andado! Pois agora, temos a parte da energia cinética que realmente irá variar devido ao trabalho da força! No entanto, precisamos obter a velocidade com a qual a bola de neve chegará ao chão! Tem alguma ideia de como fazer isso? Vem comigo!
Passo 3
A primeira coisa a se notar é que, como não temos forças dissipativas, após lançar a bolinha para cima ela irá chegar a uma altura máxima quando irá parar, quando voltar a cair na altura ela estará com a mesma velocidade inicial com a qual começou a subir, portanto, a variação da energia cinética neste intervalo é nula. E, só precisamos considerar os instantes posteriores!
Agora, do topo do penhasco até o chão, temos um deslocamento de e temos também uma aceleração constante de . A velocidade inicial é a componente vertical . E, portanto, podemos utilizar Torricelli para obter a velocidade final
Ou seja, nossa velocidade final é
Calculando então a variação da energia cinética, temos que
Que resulta em
Portanto, pelo teorema da energia cinética, temos que
Agora vamos utilizar esta informação para encontrar a próxima alternativa! Bora!
Passo 4
Como a força gravitacional é uma força conservativa, temos que
Nós obtivemos o trabalho na alternativa anterior como , e portanto, temos que
Vamos trabalhar agora com a alternativa . Vem comigo!
Passo 5
A alternativa é uma mudança de referencial, agora iremos tomar que a energia potencial está relacionada a altura . No entanto, mudar o referencial não deveria mudar a variação da energia potencial. Portanto, temos que
Usando que
O sistema se inicia no topo do penhasco, que agora está relacionado a uma energia potencial , portanto, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!