Na figura abaixo um motor exerce uma força constante para a direita sobre uma massa que cai livremente e que se encontrava inicialmente em repouso. Não há força de resistência do ar nem atrito.
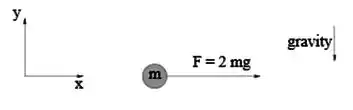
O objeto:
a) se move em linha reta com aceleração igual a .
b) se move em linha reta com aceleração igual a.
c) se move numa trajetória parabólica com aceleração igual a .
d) se move numa trajetória parabólica com aceleração igual a .
e) não é possível calcular a trajetória ou a magnitude da aceleração com os dados fornecidos pelo problema.
Passo 1
A força resultante que atuará no objeto será:
A aceleração resultante será então.
O módulo da aceleração será:
Passo 2
Agora temos que saber se ele se move numa trajetória parabólica ou reta. A trajetória parabólica acontece no lançamento obliquo, porque a única força atuando é a para baixo, ela serve como uma espécie de força centrípeta. Nesse caso temos duas forças constantes atuando. Então o objeto irá seguir no sentido da resultante dessas forças, que é uma reta na diagonal.
Resposta
Letra (b)