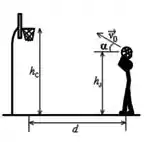
Na figura abaixo, o jogador precisa lançar a bola com um vetor velocidade inicial correto (isto é, módulo, direção e sentido corretos) para conseguir acertar a cesta. O vetor possui módulo e forma um ângulo com a direção horizontal. O jogador está a uma distância horizontal da cesta, lança a bola de uma altura , e a cesta está a uma altura . Despreze a resistência do ar e efeitos devido à rotação da bola. Considere , .
a) Encontre uma expressão para o valor do módulo de modo que a bola atinja a cesta.
b) Se , escreva os vetores velocidade e aceleração da bola no instante em que ela atinge a cesta.
c) Se pudermos variar o ângulo e a velocidade inicial, determine geometricamente qual o critério adicional devemos considerar para que a bola entre na cesta, considerando que além de alcançá-la a bola deverá necessariamente estar na descendente.
Passo 1
Pra começar vamos escrever a equação do movimento de cada eixo: e .
Vamos considerar o eixo x orientado para a esquerda e o eixo y orientado para cima.
Pra velocidade inicial em cada eixo, vamos ter:
No eixo , não vamos ter aceleração nenhuma. No eixo , a aceleração vai ser a própria gravidade.
Sendo assim, cada equação de posição da bola fica:
Reparem que nessa equação eu considerei a altura que ele vai partir como se fosse , ok? Então tem que tomar cuidado na hora que for escrever a altura!
Passo 2
Letra a)
Se ele deu pra gente o valor de e em um mesmo instante, ficamos com duas incógnitas: .
Como queremos o , vamos isolar o e substituir na equação de :
Substituindo na equação de , vamos ficar com isso aqui:
Isolando o nosso :
Passo 3
Letra b)
Primeramente, vamos calcular esse pra sabermos o módulo da velocidade inicial:
Agora, precisamos do tempo que a bola atinge a cesta, fechou?
Vamos usar a equação no eixo que é bem mais fácil, já que não envolve aceleração nem nada.
Como sabemos o valor de , e o valor do , quando substituímos, ficamos com:
Agora, vamos calcular as componentes do vetor velocidade. Vamos dividir em duas partes como sempre: .
Eixo :
Como não tem aceleração, a velocidade vai ser sempre constante:
Eixo :
Já no eixo vamos ter que usar a equação da velocidade, porque temos a aceleração negativa da gravidade:
O vetor velocidade é dado por:
O vetor aceleração continua sempre sendo:
Passo 4
Letra c)
Bom, primeiro vamos achar a relação para o movimento ser descendente com o ângulo do lançamento, ok?
Sabemos que o movimento é descendente quando a velocidade de , passa a ser negativa. Ou seja, precisamos saber o ponto que a velocidade muda de sentido.
Como sabemos que a cesta está a uma distância do lançamento, podemos fazer uma relação com também.
Ou seja:
Resposta
a)
b) ; .
c)