Um projétil é lançado com velocidade formando um ângulo com a horizontal. O ponto de lançamento está localizado a uma altura acima do solo. A figura mostra o sistema de referencia fixo, que está localizado no solo e tem eixo vertical alinhado verticalmente com o ponto de lançamento. De acordo com este referencial, pressupondo que a resistência do ar é desprezível e que a Terra é um referencial Inercial:
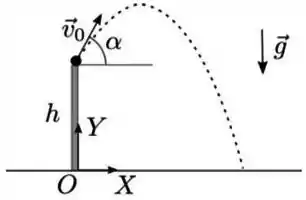
Escreve os vetores posição e velocidade , como funções do tempo , usando os unitários e dos eixos e , respectivamente, indicados na figura;
Calcule o tempo que o projétil leva para atingir a altura máxima;
Calcule o tempo de vôo do projétil.
Determine, quando o projétil toca o solo, o módulo da sua velocidade .
Passo 1
Vamos começar o problema escrevendo os dados do enunciado
Isso vai servir para conferirmos depois se as respostas estão de acordo com os dados do enunciado.
A gravidade é negativa, porque ela é para baixo, lembra? Cuidado com os sinais!!
Passo 2
Para escrevermos os vetores posição e velocidade, devemos achar a posição e velocidade ao longo do tempo do movimento ao longo de e ao longo de.
No eixo temos um Movimento Uniforme.
No eixo , temos um lançamento vertical, que neste caso é um lançamento vertical para cima.
A primeira coisa a fazer é encontrar e
Usando a “regra do COlado, SEparado” vamos ter
Ambos são positivos, porque a velocidade está para direita e para cima.
Passo 3
Vamos agora escrever as equações da posição pelo tempo, começando pelo movimento ao longo de
Passo 4
Para o movimento ao longo de
Passo 5
Lembra como escrevemos esse vetor agora?
Ele fica:
Passo 6
Vamos agora escrever as equações da velocidade pelo tempo, começando de novo pelo movimento ao longo de , como o movimento é uniforme temos que:
Logo,
Passo 7
Para o movimento acelerado ao longo de
Passo 8
O vetor velocidade representado por unitários fica da seguinte forma:
Passo 9
Ele quer o tempo que o projétil gasta para atingir a altura máxima. Isso vai acontecer quando a velocidade em é zero. Então devemos fazer
Passo 10
O tempo de vôo vai ser o tempo que ele demora para chegar ao chão. O que isso quer dizer?
Que o valor da posição na vertical é zero.
Resolvendo a equação de segundo grau
Como o tempo de vôo deve ser positivo, e o valor dentro da raiz é maior que
Passo 11
Para acharmos o módulo da sua velocidade devemos achar cada componente quando o tempo for igual ao tempo de vôo. Então
Passo 12
Agora que sabemos o valor de cada componente da velocidade podemos fazer módulos dela
Lembrando que