Livro Halliday, Volume 1, 8ª Edição, Capítulo 4, Seção 6, Exercício 54
(Capítulo 4.6 – Ex.54) Dois segundos após ter sido lançado a partir do solo, um projétil deslocou-se horizontalmente e verticalmente em relação ao ponto de lançamento. Quais são as componentes (a) horizontal e (b) vertical da velocidade inicial do projétil? (c) Qual é o deslocamento horizontal em relação ao ponto de lançamento no instante em que o projétil atinge a altura máxima em relação ao solo?
Passo 1
Faaaala, pessoal! Tudo certinho? Bora lá resolver mais uma questão!
Então, antes de qualquer coisa, a gente precisa entender o que está acontecendo com o projétil, pra gente conseguir saber o que e como vamos calcular o que é pedido.
Vamos lá então! A gente sabe que o projétil foi lançado a partir do solo. Então, se formos desenhar a sua trajetória, vamos ter algo mais ou menos assim:
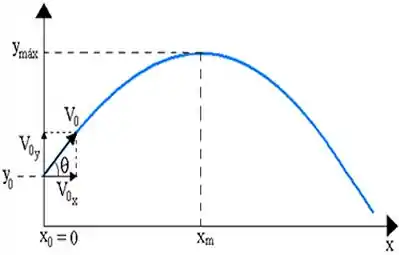
Nessa figura, vamos assumir que o eixo x corresponde ao deslocamento na horizontal, e que o eixo y representa o deslocamento na vertical. Além disso, vemos que existe a decomposição da velocidade em x e y (horizontal e vertical).
Então pessoal, vamos começar resolvendo o item (a).
Como o movimento horizontal é uniforme, podemos assumir que:
Onde é o deslocamento, a velocidade na componente horizontal e o tempo. Dessa forma:
Prontinho! Bora pro item (b)!
Passo 2
Nesse item, temos que perceber que o movimento vertical é uniformemente variado, já que vamos ter a atuação da gravidade, beleza?
Então, vamos ter que a velocidade na componente vertical se dá por:
Passo 3
Por fim, pra gente encontrar o deslocamento horizontal pedido no item (c), devemos primeiro achar o tempo que o projétil leva até chegar na altura máxima.
Isso pode ser feito através da relação:
Como a componente horizontal da velocidade é constante , temos que:
Prontinho! Conseguimos!
De boa, galera?? Bora resolver mais uma questãozinha?
Resposta
a)
b)
c)