Um jogador de futebol bate uma falta, fazendo com que a bola saia com velocidade inicial , do solo, fazendo um ângulo de . Sabendo que um vento sopra da esquerda para direita, imprimindo uma aceleração nessa direção com módulo igual ao módulo da gravidade. Determine a altura máxima do chute, e seu alcance. Na frente do jogador, a , está um gol com de altura. Determine se a bola vai na direção do gol, passa por cima dele, ou cai antes do gol.
Dados: , 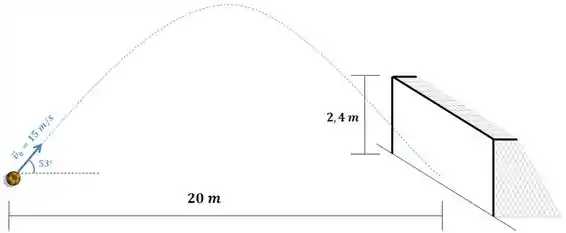
Passo 1
No enunciado, a bola é chutada para cima. Então:
No eixo , temos um lançamento vertical, que neste caso é um lançamento vertical para cima.
No eixo , nesse caso, temos aceleração então ele é um Movimento Uniformemente variado.
Pelo enunciado teremos:
Vamos primeiro achar as componentes da velocidade inicial, pela regra do “COlado/Separado”:
Passo 2
Para achar a altura máxima, estamos usando o movimento na vertical.
O que acontece quando a bola está na altura máxima? , como em temos um e queremos a posição, vamos usar a equação de Torricelli.
Passo 3
Para encontrarmos o alcance, primeiro devemos achar o tempo que ele demora para chegar ao chão, ou seja, quando
Resolvendo a equação do 2º grau, vamos encontrar dois valores para essa equação, mas lembre
O tempo não é negativo, TEMPO SEMPRE POSITIVO.
Passo 4
Agora usamos esse tempo na equação da posição do eixo . Lembrando que ele é um MUV
Passo 5
Para descobrir onde a bola passou, devemos achar a altura da bola quando ela passa pelo gol.
Primeiro vamos achar o tempo para ela chegar ao gol, saberemos isso pela posição do gol no eixo . Como temos o vento soprando para a direita, imprimindo uma aceleração constante de módulo igual à da gravidade, a gente tem
De novo caímos em uma equação do segundo grau. Resolvendo, e lembrando que
O tempo não é negativo, TEMPO SEMPRE POSITIVO.
A gente descobre que
Passo 6
Vamos agora descobrir a altura que a bola se encontra ao passar pela possição do gol.
A altura do gol é , como a bola passa a do chão, o jogador errou o chute no gol.
Repare que a aceleração do eixo não interfere em nada no movimento do eixo e vice versa.
Resposta
, ele erra o chute no gol.