Um projétil é lançado do nível do chão com uma rapidez inicial de . Encontre o ângulo de lançamento ( o ângulo que a velocidade inicial forma acima da horizontal) de forma que a altura máxima do projétil seja igual ao seu alcance horizontal. (Ignore a resistência do ar.)
Passo 1
Vamos entender o problema fazendo um desenho da situação, o projétil é lançado com velocidade e o problema pede o ângulo de inclinação para que o alcance e a altura sejam iguais, dessa forma temos a seguinte situação.
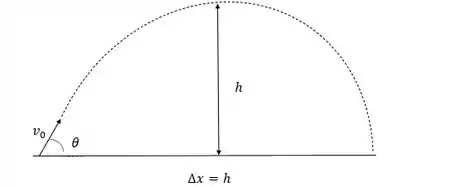
Beleza, se eu sei disso agora preciso encontrar uma relação entre a altura e o alcance , vamos fazer isso decompondo a velocidade e analisando os dois movimentos, vertical e horizontal.
Passo 2
Vamos decompor as velocidades, usando as seguintes relações:
E aqui separamos os movimentos, o movimento horizontal é um movimento uniforme e portanto o alcance é dado por:
Aonde é o tempo total do movimento, isso é, até o projétil chegar ao solo.
Já o movimento vertical é um pouquinho diferente, temos a gravidade desacelerando, portanto temos um movimento uniformemente variado. Pra encontrar a altura máxima, podemos aplicar a equação de torricelli.
Só que aqui a velocidade no ponto da altura máxima é e portanto:
Isolando e lembrando que
Agora é só igualar as equações para esses carinhas aqui:
Cortando os termos semelhantes temos o seguinte:
Putz, mas e esse aí, o que eu faço com ele?
Ele é o tempo total do lançamento, e é o único termo que a gente não tem.
Muita calma nessa hora, vamos dar um jeitinho nisso.
Passo 3
Para encontrarmos o tempo vamos analisar o movimento vertical, se a gente pensar na subida poderemos ver pela equação da velocidade quem é esse cara:
Onde
Já que o movimento completo leva em consideração subida e descida. Aqui sabemos também que na altura máxima a velocidade final na vertical é e então a equação fica:
Rearrumando temos então o querido tempo!
Agora é só voltar na nossa equação antiga e substituir essa galera aí:
Daí pegue a tesoura pois cortaremos muita gente por aqui hehe!

Cortando e de ambos os lados e também o que passará a ser , temos:
E se liga aí, essa relação que temos é a tangente!
Agora é só inverter e já era:
Resposta