Um canhão antitanque está localizado na borda de um platô a acima de uma planície, conforme a figura abaixo. A equipe do canhão avista um tanque inimigo parado na planície à distância de do canhão. No mesmo instante, a equipe do tanque avista o canhão e começa a se mover em linha reta para longe deste. com aceleração de . O canhão antitanque dispara um projétil com velocidade de disparo de e com ângulo de acima da horizontal.

Quanto tempo a equipe do canhão teria de esperar antes de atirar, se quiser acertar o tanque?

Com que ângulo o projétil atinge o tanque?

Para começar vamos analisar o movimento do projétil nas duas direções! Primeiro, temos que na vertical, a força peso dada por

sempre aponta para baixo e é a única força atuando nesta situação. Portanto, na vertical, temos o movimento de uma partícula que tem aceleração constante . Portanto, a equação horária é dada por

mas quem são e ? O vetor posição inicial é dado simplesmente pela altura da planície em um referencial em que a base da planície é a origem, portanto, temos que

A velocidade inicial é um pouco mais complicada! Note que a velocidade inicial é um vetor que faz um ângulo de com a horizontal, portanto, nós formamos o seguinte triângulo retângulo

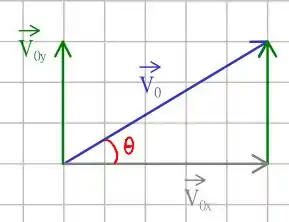
Portanto, temos que a velocidade inicial vertical é dada por

em que e Ou seja, verticalmente a bala de canhão se move obedecendo que

Vamos fazer agora a análise do movimento na horizontal! Saca só!

Diferentemente da vertical, neste caso idealizado, não existem forças que atuam horizontalmente, portanto, não há aceleração, e a equação horária toma a forma

em nossa escolha de referencial temos que e também, pelo triângulo retângulo no passo anterior, temos que

e, a equação horária toma a forma

Em alguns exercícios é conveniente isolar o tempo em termos do vetor e utilizar esta informação para escrever a equação da trajetória em conjunto com . Mas, para este problema, será conveniente manter as equações desta maneira! Vamos utilizar esta expressão para calcular o alcance de nosso canhão!

O que é o alcance em um lançamento oblíquo? É o quão longe o projétil consegue ir antes de cair novamente no chão, ou seja, qual o valor de quando ? Se usarmos a nossa equação do vetor posição vertical para obter o instante de tempo em que isso acontece, temos que

Temos um polinômio de segundo grau em , se aplicarmos Bhaskara, temos as seguinte raízes

usando uma calculadora para facilitar a nossa vida, podemos obter que

ou, simplesmente, temos que , que é um valor negativo, e portanto, vamos ignorá-la, já que o tempo em geral é um valor positivo. A outra raiz será

O nossa alcance será então dado pelo valor do vetor em . Bora lá!

Usando o valor que calculamos para o tempo na equação para a posição do projétil horizontal, temos que

aproximando o valor do cosseno, temos que

Ou seja, nós estamos errando o tanque por aproximadamente . Temos que o tanque inicialmente estava em . E, nos é dito no enunciado que ele se move para longe do canhão com uma aceleração de . O tempo que o atirador deve esperar para atirar é o tempo que o tanque (partindo do repouso) vai levar para percorrer os ! Vamos calcular isso agora!

Como tanque parte do repouso, e tem uma aceleração constante, sua equação do movimento será

agora temos que , e também que o tanque parte do repouso, portanto . Ou seja, a equação do movimento pode ser escrita como

Se calcularmos o tempo para que , temos que

Isolando , temos que

ignorando novamente o valor negativo para o tempo, temos que

que é quanto tempo o atirador deve esperar para atirar! E, a resposta de nossa primeira alternativa! Vamos para a segunda agora!

Nós temos que o vetor velocidade é formado por uma combinação das suas componentes verticais e horizontais, como vimos no triângulo retângulo lá atrás! Quando o projétil atinge o tanque, nós temos um novo triângulo da seguinte forma

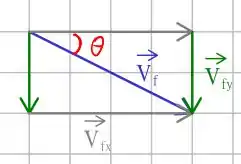
Portanto, precisamos calcular as componentes finais da velocidade e usar relações trigonométricas para achar o novo ângulo . Como o projétil não sofre influências de forças na horizontal, a sua componente horizontal da velocidade é constante, ou seja, temos que

ou, aproximadamente

A componente vertical vai precisar de uma atenção um pouco maior! Vamos trabalhar um pouquinho com ela!

Note que a componente vertical tem uma aceleração constante, no entanto, a aceleração é negativa até a partícula atingir a altitude máxima, e é positiva pelo resto da trajetória! O que nos dará a velocidade desejada é o segundo movimento, mas ele é um movimento da forma

e qual é esse tempo? É o tempo que o projétil leva da altura máxima até atingir o tanque! Ou seja, queremos obter este tempo a partir da relação

Note que estou colocando a velocidade inicial como , isso é porque estas equações estão considerando o movimento a partir da altura máxima, ou seja, quando a partícula pára de subir no topo da trajetória! Tudo bem, mas e quem é ??? Vamos achar ele antes de qualquer coisa!

Para achar o valor da altura máxima vamos ter que analisar a evolução da velocidade na subida do projétil, ou seja, a nossa velocidade é dada por

a altura máxima pode ser obtida avaliando no instante de tempo em que da subida vai a zero. Portanto, igualando a equação acima à zero, temos que

e, portanto, a altura máxima é tal que

ou, simplesmente, temos que

Maravilha! Vamos usar isso para calcular a nossa velocidade final! Saca só!

Primeiro, precisamos obter o tempo necessário para que a seguinte relação seja verdade

usando . Podemos isolar o tempo como

e, tirando a raiz, temos que

Portanto, a velocidade final será

Uff… finalmente temos os dois vetores! Vamos achar o nosso ângulo agora! Bora bora!

Usando o triângulo retângulo que tínhamos montado anteriormente, temos que

usando os vetores que calculamos, temos que

ou seja, temos que o ângulo é

ou, em graus, temos que

A questão foi isso! Te vejo na próxima! Tchau Tchau!