Num jogo de futebol, um jogador chuta a bola em direção ao gol com uma velocidade inicial que faz um ângulo com a direção horizontal. Despreze a resistência do ar e trate a bola como um objeto pontual. Suponha que o gol esteja a uma distância horizontal do ponto do chute, e possua altura, conforme figura abaixo.
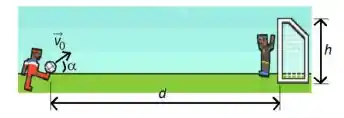
d) Considerando o mesmo valor de encontrado no item (a), escreva uma equação que permita encontrar outro valor de que também faz a bola acertar o travessão (não precisa resolver a equação).
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um exemplo clássico de movimento oblíquo de um jogador chutando uma bola ao gol.
A questão nos pede o ângulo em que a bola atinge a trave superior e também nos pergunta se ela atinge a trave superior durante sua subida ou descida.
Uma dica é analisarmos a composição do movimento horizontal e do movimento oblíquo na trajetória da bola.
E aí? Bora lá?
Passo 2
Bom... Pelo lançamento horizontal, temos o tempo em que a bola leva para percorrer os :
Passo 3
Assim, pelo movimento vertical, temos:
Substituindo e demais valores:
Entendeu direitinho? Responde aee ;)
