Exercícios Resolvidos de Mostrar que o Limite Não Existe em Funções de Várias Variáveis
Ver TeoriaEnunciado
Calcule , o limite, quando existir. Caso contrário, justifique.
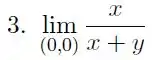
Passo 1
Vamos começar, como sempre, tentando substituir o ponto :
Ops, deu indeterminação .
O próximo passo agora é então tentar sair desse negócio pra vê se a gente consegue ou não calcular esse limite.
Passo 2
Hum, mas olha só esse grau do numerador igualzinho ao grau do denominador .
Mó carão de que esse limite não existe, né?
Vamos tentar provar isso então, calculando por caminhos diferentes.
Primeiro vamos tentar o caminho mais intuitivo de todos :
Passo 3
Tá, agora vamos tentar o caminho :
Uhul, deu diferente!
Isso significa então que nosso limite não existe.
Resposta
Exercícios de Livros Relacionados
Determine o limite, se existir, ou mostre que o limite não existe. lim x , y , z → 0,0 , 0 x y + y z x 2 + y 2 + z 2
Determine o limite, se existir, ou mostre que o limite não existe. lim x , y → ( 1,2 ) ( 5 x 3 - x 2 y 2 )
Determine o limite, se existir, ou mostre que o limite não existe. lim x , y , z → π , θ , 1 e y 2 t g ( x z )
Determine o limite, se existir, ou mostre que o limite não existe. lim x , y → ( 1,0 ) x y - y x - 1 2 + y 2
Determine o limite, se existir, ou mostre que o limite não existe. lim x , y → 0,0 x 2 + s e n 2 y 2 x 2 + y 2