Exercícios Resolvidos de Mostrar que o Limite Não Existe em Funções de Várias Variáveis
Ver TeoriaEnunciado
Considere a função
- Determine e esboce o domínio de
- Determine as curvas de nível e de , esboçando-as na mesma figura de .
- Existe ? Justifique.
Passo 1
Falou de domínio precisamos olhar as restrições.
Aqui, temos uma fração, então
Ou seja, o domínio é todo o , exceto as duas retas que passam pela origem.
Passo 2
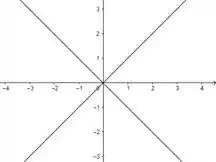
Desenhando esse negócio, temos
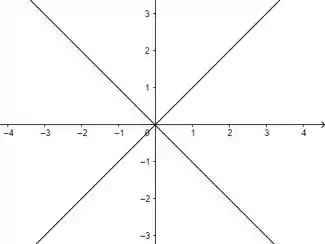
Aí o ideal na sua prova seeria você desenhar essas retas tracejadinho, tá bem? Pra mostrar que elas NÃO fazem parte do dominio.
Passo 3
Agora vamos para as curvas de nível.
Basta igualar nossa função aos níveis pedidos.
Começando com :
E temos que a curva de nível um da função é um par de retas paralelas nos níveis .
Desenhando na mesma figura que o domínio da letra , temos:
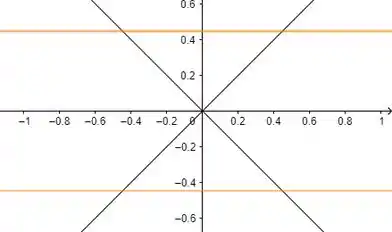
Passo 4
Agora a curva de nível :
E temos que a curva de nível zero da função é uma elipse.
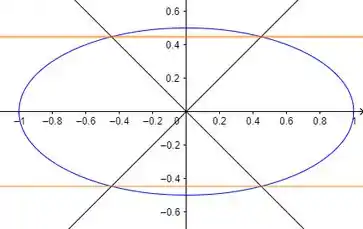
Desenhando na mesma figura que o domínio da letra , temos:
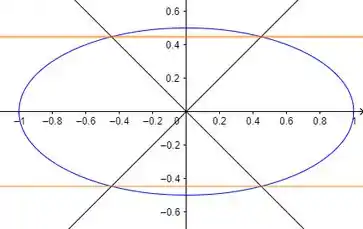
Fica ligado que os pontos tanto da elipse azul, quanto do par de retas laranja, que estão sobre o par de retas pretas (que representam o domínio) NÃO fazem parte da curva de nível, pois essas retas pretas estão fora do domínio.
Passo 5
Vamos tentar calcular
Bom, temos um gráfico com curvas de nível da função desenhados nele. Vamos ver se a gente consegue ver algo relacionado ao valor que a função tende quando através das curvas de nível.
Ou seja, vamos tentar resolver esse limite graficamente.
Pra facilitar, vou marcar esse ponto ali na nossa figura:
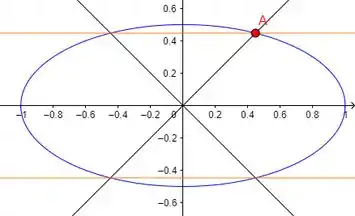
Se você reparar, esse ponto é bem num lugar onde tem vários (dois kkk) caminhos passando, que são as curvas de nível.
O caminho preto não conta, ele serve só pra nos mostrar que esse ponto seria um ponto problemático pra calcular esse limite porque tá fora do domínio da função então daria alguma indeterminação na hora de calcular e tal... Mas isso já pode ser um indício de que talvez esse limite aí nesse ponto não exista.
E de fato, se a gente for esperto, curva de nível é nada mais nada menos do que o conjunto de todos os pontos onde a função vale A MESMA COISA. E a nossa função pode tender aquele ponto A através da curva de nível azul, onde ela vale , e também pode tender aquele ponto através do caminho da curva de nível laranja, onde ela vale .
Então quer dizer, ela pode tender aquele ponto por pelo menos dois caminhos diferentes e por cada um desses caminhos ela vale uma coisa diferente.
Isso significa que esse limite não pode existir!!
Resposta
Não, pois a função tende a valores diferentes ao longo das curvas de nível quando se aproxima do ponto .