Exercícios Resolvidos de Mostrar que o Limite Não Existe em Funções de Várias Variáveis
Ver TeoriaEnunciado
Calcule , o limite, quando existir. Caso contrário, justifique.
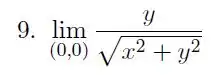
Passo 1
Vamos começar substituindo :
Êê, para nossa alegria (sqn), caímos numa indeterminação ☹
Beleza, vamo ver se a gente pode sair dela.
Passo 2
Só olhando por alto pra esse limite a gente não consegue ter nem uma ideia do que podemos fazer pra resolver esse problema da indeterminação.
Mas, uma boa dica é lembrar que, quando temos uma raiz quadrada de um número elevado ao quadrado, a gente sempre vai ter como resultado o módulo desse número.
E módulo significa então que nossa fração vai poder ser positiva ou negativa. Ou seja, nosso limite vai ter dois valores diferentes.
E isso lembra aquela parada de que se calculamos o limite por caminhos diferentes e o resultado dá diferente, é porque o limite não existe.
Vamos tentar seguir essa linha de raciocínio então.
Passo 3
Vamos tentar fazer o caminho :
Se , então temos:
Já se , temos:
Ou seja, dois resultados diferentes.
Esse limite então não pode existir.