Considere a função e seja a curva de nível de que passa pelo ponto .
- Represente geometricamente o domínio de e Faça um esboço da curva .
- Determine uma parametrização para a curva , isto é, encontre um intervalo e uma função contínua cuja imagem é .
- Decida se existe
Passo 1
a) Para determinarmos o domínio de uma função, devemos procurar por “problemas” que poderíamos vir a ter. Nesse caso, o único fator que limita o domínio da função é a raiz quadrada no denominador, que deve sempre ser maior que (pois está no denominador, e não poderia ser menor que porque é uma raiz). Assim, podemos afirmar que:
E desenvolvendo, teremos:
E o nosso domínio fica sendo o conjuntos dos pontos tais que .
Passo 2
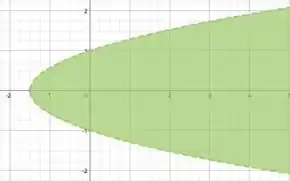
Como o enunciado pede pra dar a interpretação geométrica do domínio, é só a gente esboçar a curva e depois pegar a região denotada por .
Bom, temos um termo isolado de potência e outro ao quadrado do lado direito. Isso só pode ser uma parábola!! De fato, é uma parábola, mas deitada (perceba, temos em função de , é uma parábola com os eixos trocados ;) ), com o vértice em e apontando no sentido positivo do eixo . Podemos concluir esses dois últimos fatos porque o coeficiente de é positivo, e se fizermos temos !
Assim, nossa curva é a parábola:
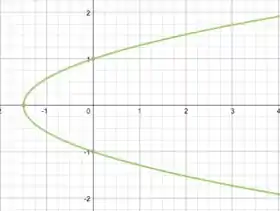
E a região que encontramos para o domínio é , ou seja, os pontos sempre a direita da linha da parábola, excluindo a própria linha, pois o sinal é de e não
Passo 3
Agora temos que encontrar essa curva de nível que contém o ponto . Bom, antes de mais nada, temos que descobrir qual é esse nível!!
Para isso, basta substituirmos o ponto dado na função. Fica assim:
Simples assim!
Passo 4
Agora que temos o nível, vamos igualar a função a essa constante, e então encontrar a equação para a curva .
Aqui vem um detalhe importante, perceba que o é igual a uma raiz! Só por isso já poderíamos afirmar que . Mas acontece que o argumento da raiz quadrada tem umas particularidades. Veja que se colocássemos , teríamos , ou seja, sobre alguma coisa dá ! Então não seria uma curva de nível , pois o valor de seria , e o não conseguiria “compensar”.
Continuando...
Podemos completar o quadrado para o , somando de cada lado:
E eis aí equação da nossa curva !! Vamos ver que curva é essa?
Passo 5
Temos a curva:
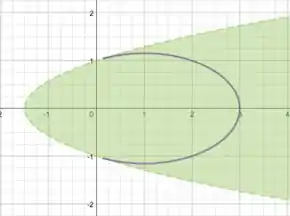
Que tem ambas as variáveis somadas e elevadas ao quadrado. E, além disso, os denominadores dessas variáveis são diferentes... É uma elipse! Veja, pela equação da elipse fica mais fácil de perceber:
Sendo que seus vértices estão em e , ou seja, e .
Mas, não esqueça do que falamos ali em cima, !! Então, na prática, temos uma parte da elipse, apenas. Que é a do lado positivo do eixo :
Passo 6
b) Vamos parametrizar essa “elipse”? Bom, me parece mais fácil parametrizar a elipse toda, como se não tivéssemos essa parada de , e depois restringir o parâmetro. Vamos lá?
Se temos uma elipse genérica, , então sabemos que sua parametrização é:
Então, olhando pra isso, a parametrização da nossa elipse será:
Passo 7
Legal, agora temos que adicionar a restrição para completar a parametriza��ão! Como e , temos que .
Assim, prosseguimos dizendo que e, portanto, . Para atender a este requisito, deve estar entre e .
E a parametrização fica sendo:
Passo 8
- Vamos ver agora se existe.
Da equação do enunciado, temos:
Agora vamos testar o limite pela curva . Assim, teremos e :
Ok, acabamos de ver que, por essa curva, teremos um limite que vale .
Passo 9
Agora, vamos, por exemplo, testar a curva do item , que, afinal, está contida na superfície de , por ser uma curva de nível!
Para que na curva , teremos que:
E, apenas conferindo, se colocarmos para a coordenada , teremos:
Ou seja, temos o ponto quando o parâmetro vale .
Então, o limite será:
Mas calma, a curva não é uma curva de nível da função? Então, sabemos que o valor da função para qualquer ponto dessa curva é o valor do nível! Ou seja, !
Então, o limite fica sendo:
E acabamos de provar que o limite não existe! Pois se por uma curva ele assume um valor e por outra assume outro, então ele não existe ;)
Resposta
a) 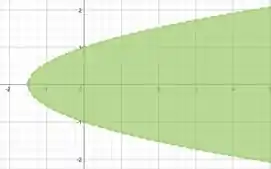
b)
c)O limite não existe, pois encontramos dois valores diferentes para ele em duas curvas diferentes