Exercícios Resolvidos de Mostrar que o Limite Não Existe em Funções de Várias Variáveis

Ver Teoria

Exercício 58 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 59 60 61 62 63 64 65 66 67

Enunciado

Calcule , o limite, quando existir. Caso contrário, justifique.

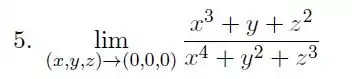
Passo 1

Vamos começar, tentando substituir o ponto :

Ops, deu indeterminação .

O próximo passo agora é então tentar sair desse negócio pra ver se a gente consegue ou não calcular esse limite.

Passo 2

Aqui temos o grau do numerador menor que o grau do denominador . Além disso, temos , e com expoentes diferentes, somados, tanto no numerador quanto no denominador.

Tudo isso são bons indicios de que o limite não existe.

Vamos tentar provar isso então, calculando por caminhos diferentes.

Primeiro vamos tentar o caminho mais intuitivo de todos :

Cortando tudo, ficamos com

Quando o , esse limite aí vai pro infinito.

Então, nosso limite não existe e dessa vez nem precisamos tentar calcular por mais de um caminho.

Resposta

Exercícios de Livros Relacionados

Determine o limite, se existir, ou mostre que o limite não existe. lim x , y , z → 0,0 , 0 ⁡ x y + y z x 2 + y 2 + z 2

Determine o limite, se existir, ou mostre que o limite não existe. lim x , y → ( 1,2 ) ⁡ ( 5 x 3 - x 2 y 2 )

Determine o limite, se existir, ou mostre que o limite não existe. lim x , y , z → π , θ , 1 ⁡ e y 2 t g ( x z )

Determine o limite, se existir, ou mostre que o limite não existe. lim x , y → ( 1,0 ) ⁡ x y - y x - 1 2 + y 2

Determine o limite, se existir, ou mostre que o limite não existe. lim x , y → 0,0 ⁡ x 2 + s e n 2 y 2 x 2 + y 2