Exercícios Resolvidos de Mostrar que o Limite Não Existe em Funções de Várias Variáveis
Ver TeoriaEnunciado
Considere a função de duas variáveis:
1. Qual domínio dessa função? Descreva-o algebricamente e também faça um esboço.
2. Calcule, se existir, o limite abaixo. Caso nã exista, justifique.
Passo 1
Para analizarmos o domínio vale lembrar que não podemos ter raízes de número negativo e nem divisão por zero, certo?
Então teremos:
O domínio também vai ser bem simples:
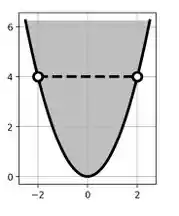
Eu tenho que nosso y deve ser diferente de 4, por essa razão temos aquela linha pontilhada ali...ou seja, não entra nada dela ali no domínio, e temos ainda que o y deve ser maior ou igual à , ou seja, tudo acima e em cima da parábula, já que são valores maiores (acima) e iguais (na parábula) a .
Escrevendo o domínio matematicamente temos:
Passo 2
Para calcular esse limite, fazemos primeiro o limite em cima da parábula, ou seja, quando
Observando agora o limite ao longo da semi reta (para ) temos:
Como nosso y está indo pra 4 temos:
Observa como os resultados estão distuando. Isso significa então que esse limite não existe. Caso obtivéssemos valores iguais, teríamos então um resultado para esse limite, como não aconteceu, o limite não existe.