Exercícios Resolvidos de Mostrar que o Limite Não Existe em Funções de Várias Variáveis
Ver TeoriaEnunciado
Considere a função
- Determine o domínio de
- Encontre uma equação para as curvas de nível e de . Esboce tais curvas no sistema cartesiano.
- Existe ? Justifique sua resposta.
Passo 1
Falou em domínio, a primeira coisa que tem que vir na nossa cabeça é RESTRIÇÃO.
Nesse caso, temos uma fração, então o denominador tem que ser diferente de zero:
Assim, o domínio da nossa função é:
Que corresponde a todo o plano, exceto os pontos que estiverem sobre a circunferência
Passo 2
Ótimo! Agora vamos determinar as curvas de nível.
Para isso, basta igualarmos a expressão da função aos valores de pedidos.
Mas, antes, vale lembrar que se a função não estiver definida num ponto, nenhuma curva de nível poderá passar por ele.
Beleza, então, para , a curva de nível é:
Assim, a curva de nível de é toda a reta , exceto os pontos dessa reta que cortarem a circunferência
E esses pontos são
e .
Passo 3
Agora, para , a curva de nível é:
Assim, a curva de nível zero de é toda a hipérbole , exceto os pontos dessa hipérbole que cortarem a circunferência
E esses pontos são e .
Passo 4
Agora só nos resta esboçar tudo isso junto.
Assim, esboçando a reta (vermelha);
Esboçando a hipérbole (azul)
Cortando o eixo .
E, esboçando a circunferência (verde) que delimita o domínio
Temos
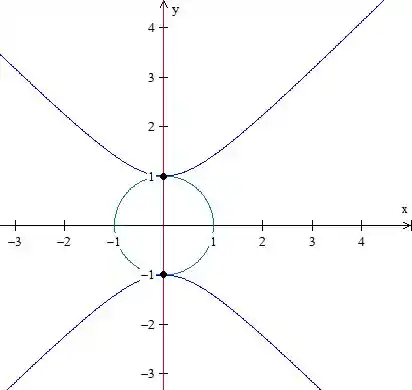
Onde os pontos marcados são pontos onde não existe curva de nível, porque a função não está definida.
Passo 5
Agora queremos saber se existe.
Vamos pensar que ele não existe. Como fazemos para provar isso?
Geralmente a gente calcula esse limite por caminhos diferentes e se obtivermos resultados diferentes, então quer dizer que o limite não existe.
Mas, nesse caso, se você reparar as curvas de nível que desenhamos na letra , vai ver que conforme nossa se aproxima do ponto , ora ela pode valer (quando está sobre a curva de nível zero), ora pode valer (quando está sobre a curva de nível ).
Ou seja, se usamos dois caminhos diferentes (curva de nível e ), nossa função tende a valores diferentes, logo, esse limite não pode existir.
Resposta
Curva de nível :
Curva de nível :
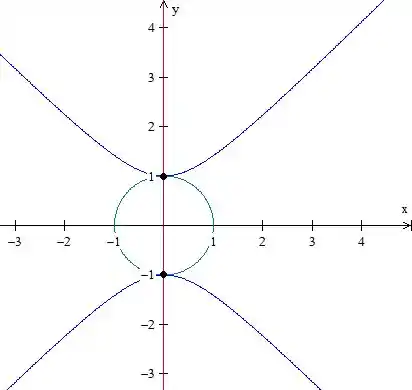
Não, pois se usamos dois caminhos diferentes (curva de nível e ), nossa função tende a valores diferentes.