A ação de uma força de módulo aplicada na direção horizontal de um bloco de massa , faz com que ele suba uum plano inclinado de com a horizontal. O coeficiente de atrito cinético entre o bloco e o plano inclinado é Durante o trajeto, o bloco se desloca ao longo do plano uma distância O bloco parte da base do plano e do repouso. Utilize:
- Calcule o trabalho efetuado por cada uma das forças que atuam no bloco durante o trajeto de subida ao longo do plano inclinado. Justifique seus cálculos.
- Calcule a variação da energia cinética durante todo o percurso. Justifique seu cálculo
- Suponha uma outra situação, onde o mesmo bloco sobe o plano inclinado sob a ação de uma outra força de módulo aplicada na direção paralela ao plano inclinado. Existe atrito entre o bloco e o plano, mas neste caso, o módulo da força de atrito cinético varia com a velocidade do bloco e é dada em Newtons por , onde é dada em . Calcule o módulo da força e a potência fornecida por ela ao bloco quando a velocidade do bloco for igual a sabendo que a aceleração do bloco ao longo do plano no mesmo instante é dada por
Passo 1
a)
Bom, primeiramente, vamos adotar eixos e , o primeiro perpendicular à superfície do plano e outro paralelo à superfície do plano.
Fica Assim:
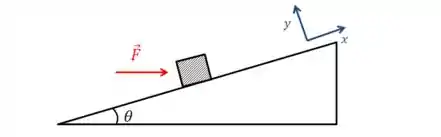
Vamos decompor primeiro a força nessas duas direções:
Qual é a componente que realiza trabalho? A componente , já que a outra é perpendicular ao movimento. Como a força é constante, o trabalho será dado por:
Aplicando os valores:
Quais são as outras forças? A força de atrito e a força peso.
Bom, a força de atrito é sempre tangente à direção do deslocamento. Ela vale:
Menos porque é contrário ao movimento. E quanto vale a normal? Vale aquele valor que a gente usa nos planos inclinados:
Assim:
Lembrando que:
Assim, o trabalho da força de atrito vale:
E o trabalho da força peso? Ahh, esse é mais fácil: Lembra que o peso é uma força conservativa e que o trabalho de forças conservativas não dependem da trajetória?
Então, você não precisa decompor o peso naquelas duas direções novas. O trabalho do peso será dado por:
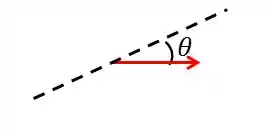
E quem vale Basta a analisar a figura abaixo:
Assim, o trabalho da força peso será:
Passo 2
b)
Podemos usar o teorema trabalho energia cinética aqui:
Então, precisamos calcular o trabalho total sobre o sistema. Esse será a soma de todos os trabalhos calculados antes. Assim:
Assim:
Observe que o termo entre os parênteses é a resultante das forças na direção
Passo 3
c)
Agora a força está na direção Assim, o trabalho dela será dado por:
E a potência média será:
Beleza, mas não sabemos o valor do módulo de Pra isso, podemos usar a segunda lei de Newton, já que temos o valor da aceleração quando
A força resultante na direção será dada por:
Veja que colocamos ali a componente do peso na direção Como é uma função da velocidade, podemos calculá-la para
E a aceleração vale . Assim:
Assim, já descobrimos o valor do módulo de
Show? Agora, pra descobrir a potência, basta a gente usar esse valor na primeira equação eu vimos:
Resposta
a)
b)
c)