Na figura temos um pequeno bloco de massa em quilogramas, que parte do ponto A numa superfície horizontal com velocidade . O percurso é sem atrito até o trecho de comprimento , em que o coeficiente de atrito cinético é . As alturas indicadas são e . Considere a origem do potencial como sendo no ponto A.
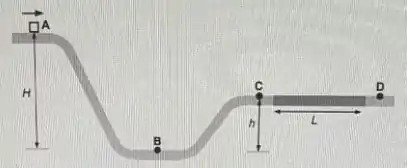
(a) Determine as energias potencial e cinética do bloco no ponto B (responda em função da massa do bloco).
(b) Determine a velocidade do bloco no ponto C.
(c) O bloco atinge o ponto D? Caso a resposta seja afirmativa, determine a velocidade do bloco nesse ponto; caso a resposta seja negativa. Calcule a distância que o bloco percorre na parte com atrito.
Passo 1
Na letra (a), queremos e .
Temos informações sobre a velocidade e altura no ponto A, então conseguimos calcular a energia nesse ponto.
Mas será que a energia mecânica se conserva ao longo do trajeto?
Em todos os pontos do trajeto do ponto A ao C, temos duas forças agindo sobre o bloco, a normal e o peso:
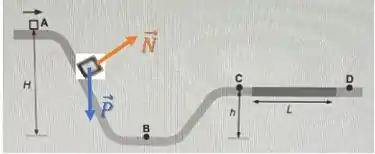
A força peso é uma força conservativa e por isso não retira energia do sistema, apenas converte energia potencial em cinética e vice-versa.
Já a força normal é uma força não-conservativa, entretanto ela não realiza trabalho, pois ela é sempre perpendicular ao deslocamento do bloquinho. Assim, a força normal também não retira energia do sistema.
Então, a resposta é sim! A energia mecância se conserva:
Passo 2
Como temos as informações sobre o bloco no ponto A, podemos igualar a energia mecânica do ponto A aos outros pontos do trajeto.
Qual é a energia mecânica em A?
Aqui temos que tomar muito cuidado com o referencial. Normalmente colocamos o referencial no ponto de menor altura do trajeto, entretanto o enunciado já define o referencial no ponto A, portanto quando o bloco desce ainda mais, ele terá uma energia potencial negativa.
Em A, o bloco terá uma energia cinética relativa a sua velocidade e sua energia potencial será nula, pois está no nosso referencial:
Passo 3
Já no ponto B, temos uma energia cinética e uma energia potencial :
Lembrando que a energia potencial em B é negativa:
Passo 4
Vamos escrever a conservação de energia:
Substituindo os valores, temos:
Como sabemos que a massa está em quilogramas (SI), podemos dizer que a energia certamente estará em :
A questão também pede o valor especificamente da energia potencial em B, que já calculamos:
Passo 5
Na letra (b), queremos a velocidade no ponto C.
Para isso, vamos conservar a energia mecânica do ponto A para o ponto C e achar a energia cinética nesse ponto .
A partir da energia cinética , conseguimos a velocidade .
Passo 6
Então, temos que:
Qual será a “altura” que o bloco está no ponto C?
Se nosso referencial está no ponto A, ele desceu uma altura:
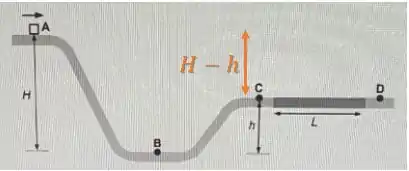
Então, temos em :
Cortando as massas, temos:
Substituindo os valores:
Passo 7
Na letra (c), queremos saber se o bloco chega no ponto D ou não.
Se a energia se conservasse de C a D, teríamos a seguinte equação:
Como eles estão na mesma altura, a energia potencial dos dois é igual, então:
Porémmmm, temos um trecho com atrito entre os dois pontos, assim, o trabalho da força de atrito irá retirar energia do sistema conforme o bloco anda.
Queremos saber se ele chega ao outro lado.
Para saber isso podemos calcular quanto de energia a força de atrito retira do sistema ao longo desse trajeto . Aí vamos olhar para a energia cinética em C .
Se for menor que , o bloco não tem energia suficiente para passar o trecho e vai parar antes de D.
Se for maior que , o bloco tem energia suficiente para passar o trecho e vai chegar em D com uma velocidade .
Passo 8
Vamos calcular .
Como a força de atrito atua contra o movimento, seu trabalho é negativo. Porém, só nos interessa o valor em si de energia retirada do sistema, ou seja vamos calcular o módulo disso:
Como o atrito é cinético, a será:
Como o bloco está em equilíbrio na vertical, a força normal será igual ao peso:
Substituindo os valores, temos:
Agora, vamos olhar para a energia cinética em C:
Opaa, como não há energia cinética suficiente, o bloco vai parar no meio do trajeto com atrito e não chegará em D.
Passo 9
Precisamos calcular qual distância o bloco percorre, então vamos usar o teorema trabalho-energia cinética:
Sendo a energia cinética final igual a zero:
Agora, vamos utilizar o sinal correto do trabalho da força de atrito:
Então a distância será:
Substituindo os valores, temos:
Então o bloco quaaaaase chega em D, mas para depois de andar .
Resposta
(a)
(b)
(c) O bloco não atinge o ponto D, ele para após percorrer .