Dois pequenos discos, de massas e , se deslocam sobre uma mesa horizontal de coeficiente de atrito cinético com os discos . Inicialmente os discos possuem velocidades em direções perpendiculares cujos módulos são desconhecidos. Em um certo instante os discos colidem e passam a se deslocar juntos. Após a colisão o sistema se movimenta em uma direção que faz um ângulo com o eixo conforme a figura. Além disso observa-se que o sistema entra em repouso após percorrer uma distância d desde o ponto onde ocorreu a colisão. Desprezando efeitos de rotação de cada disco, determine:
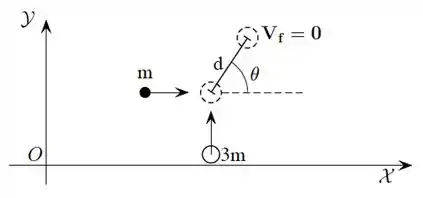
(a) O trabalho realizado pela força de atrito entre o instante da colisão e aquele em que os discos entram em repouso.
Passo 1
Analisar as forças atuando e o movimento do corpo após a colisão
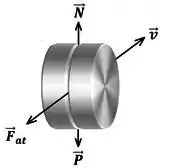
Dá uma olhada nos dois discos quando eles estão juntos. Meigo não? Sobre ele temos atuando a força peso , a força normal e a força de atrito . Como os dois discos estão juntos, a gente não vai considerar nem o peso de um nem do outro, e sim dos dois juntos, beleza?
Passo 2
Calcular o trabalho da força de atrito
O trabalho da força de atrito será então:
Mas calma, quem é esse “” aí? Esse no caso vai ser o nosso vetor deslocamento, que vai “apontar” pra onde nossos dois discos estão indo quando colados um no outro.
Como , realizando o produto escalar dos vetores, que tem direções opostas, vamos ter:
Na vertical, nada de muito especial vai acontecer. Então fique tranquilo porque na vertical basta a gente lembrar que as forças vão se anular.
O trabalho da força de atrito ficará então: