Um bloco é liberado a partir do repouso conforme a figura abaixo, iniciando seu movimento a partir da extremidade esquerda da figura. Os trechos em rampa não possuem atrito, e os trechos planos possuem atrito, com coeficiente de atrito cinético de . O valor de .
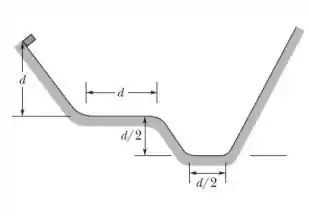
Durante seu movimento para a direita, qual a velocidade no final do primeiro trecho plano (mais alto)? Qual a velocidade no final do segundo trecho plano (mais baixo)? Qual a velocidade no final do segundo trecho plano (mais baixo)? Qual a altura máxima (em relação ao trecho plano mais baixo) que o bloco atinge na rampa da direita?
Passo 1
Oiie, tudo bem?
Temos nesta questão uma rampa formada por diversos trechos de comprimentos e alturas diferentes! Em particular temos três trechos e eles estão distribuídos como na seguinte imagem
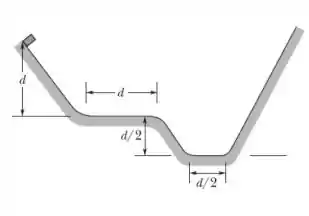
note que . Esta alternativa em particular estabelece que nosso bloquinho está se movendo para a direita, e pede algumas informações, essas são: a velocidade no final do trecho plano mais alto, a velocidade no final do trecho plano mais baixo, e por último a altura máxima que ele alcança na rampa da direita! Fazer isso é um processo de análise da energia transferida e o trabalho realizado pela força de atrito. Em geral, vamos analisar cada trecho como se a energia fosse conservada, e então reduzir a influência do atrito nos trechos planos! Belezinha? Bora lá!
Passo 2
Primeiro, as duas equações que serão úteis para nós aqui são, a expressão para a energia potencial gravitacional
em que é a massa do bloco (irrelevante para nós aqui), é a aceleração gravitacional e é a altura em um referencial de nossa escolha! Também iremos precisar da expressão para a energia cinética
em que é o módulo da velocidade que o bloco tem em algum instante específico desejado. Vamos usar também o trabalho realizado pela força de atrito
em que é o módulo da força normal atuando sobre a partícula. Como só temos atrito nas seções planas, temos que a força normal será sempre igual em módulo ao peso do bloco, ou seja
e, o trabalho da força de atrito será sempre
em que é o deslocamento do bloco na região com atrito! Maravilha! Vamos aplicar estas expressões! Saca só!
Passo 3
Inicialmente o bloco está parado no topo da rampa da esquerda, se escolhermos um referencial que a altura é na altura do trecho plano mais baixo, temos que a altura inicial do bloco é
Então, a energia inicial é totalmente potencial dada por
Parte dessa energia vai ser transformada em energia cinética ao descer a rampa, por que apenas parte? Pois nós descemos apenas uma altura , ou seja, ainda resta uma energia potencial
ou seja, quando o bloco chegar a base da primeira rampa, a sua energia será tal que
Resumindo, a energia cinética na base da rampa será
Maravilha! Isso nos dá a velocidade na base da rampa, mas nós queremos a velocidade no final do primeiro trecho plano. Consegue ver o que falta fazer? Saca só!
Passo 4
Precisamos considerar a influência do atrito na energia total do sistema ao chegar no final do primeiro trecho plano, note que este trecho tem um comprimento dado por , portanto, o trabalho realizado pelo atrito neste trecho é
este trabalho é igual a quantidade de energia que foi liberada durante o movimento, ou seja, a energia cinética restante ao final do trecho é
Isolando a nossa velocidade, temos que
ou, substituindo valores, temos que
Aí está a primeira velocidade pedida! Vamos calcular a segunda agora!
Passo 5
O bloco agora está no topo da rampa de altura com energia cinética dada pela equação , portanto, agora temos que a energia total do bloco é
ou, simplesmente, temos que
Essa energia será transformada totalmente em energia cinética, já que desce a rampa até a altura , temos então que na base da segunda rampa, temos uma energia cinética dada por
Queremos a velocidade no final deste segundo trecho plano, que tem comprimento , e portanto, o atrito realiza agora um trabalho dado por
E, a energia cinética restante, será
De forma que nossa velocidade será simplesmente
Isolando e substituindo valores, temos que
Uff… Só mais uma coisinha e essa alternativa já era! Vamos calcular a altura máxima que o bloco chega na última rampa!
Passo 6
Temos que o bloco tem uma energia cinética dada pela equação , essa energia vai ser transformar em energia potencial até parar em alguma altura da rampa, ou seja, temos que a altura máxima será dada por
Isolando a altura máxima, temos que
ou, simplesmente
Que é levemente menor do que , e significativamente menor que que é a altura inicial! Ou seja, o atrito é bastante relevante para a nossa questão! Essa alternativa já foi! Vamos para a próxima agora! Até daqui a pouco!
Resposta
, e