Trabalho e Energia Cinética
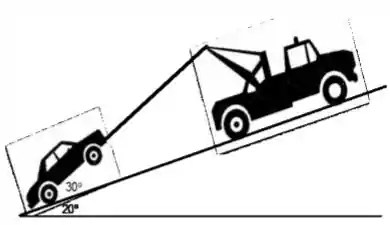
Um caminhão reboque com massa puxa, utilizando uma corrente, um carro com massa em uma ladeira com inclinação de 20° em relação à horizontal. Devido ao tipo de reboque, tanto a corrente quanto o carro ficam inclinados em relação à ladeira de 30°. As forças de atrito que atuam entre a ladeira e os pneus do carro e do reboque são respectivamente e . O reboque e o carro partem do repouso e sobem a ladeira com aceleração constante. A tensão na corrente é igual a . Após subirem , reboque e carro estão a uma velocidade . Use
a) Calcule o trabalho feito pela corrente sobre o carro após puxa-lo por ladeira acima.
b) Calcule os trabalhos da força gravitacional sobre o carro e sobre o reboque nesta mesma distância.
c) Calcule os trabalhos do atrito sobre o carro e sobre o reboque nesta mesma distância.
d) Calcule o trabalho realizado pelo motor do reboque sobre o conjunto nesta mesma distância.
Passo 1
a)
Trabalho da corrente sobre o carro:
Passo 2
b)
O centro de massa do carro e do reboque quando deslocados de uma distância ao longo do plano, têm o mesmo deslocamento na direção vertical igual a , portanto, sobre o carro:
Sobre o reboque:
Passo 3
c)
Os trabalhos do atrito são calculados da seguinte forma, sobre o carro:
Sobre o reboque:
Passo 4
d)
Aplicando o teorema trabalho-energia, sabemos que o trabalho total sobre o carro e reboque ao longo desta distância é igual à variação da energia cinética do conjunto:
Resposta
a)
b) ;
c) ;
d)