Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Atrito e Forças não Conservativas

Ver Teoria
Exercício 111234567891012131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687

Enunciado

UnB - Física 1 - Listas -Lista 8: Conservação de Energia - Questão 3

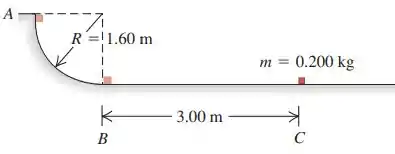
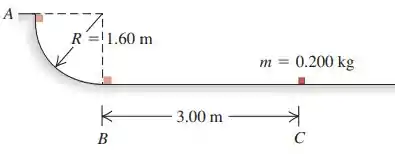
Em um posto de carga de caminhões do correio um pacote de 0.200   k g é largado do repouso no ponto A sobre um trilho com forma de um quarto de circunferência de raio igual a 1.60   m (veja a figura). O tamanho do pacote é muito menor do que 1.60   m , de modo que ele pode ser considerado como uma partícula. Ele desliza para baixo ao longo do trilho e atinge o ponto B com uma velocidade de 4,80   m / s . Depois de passar pelo ponto B , ele desliza uma distância de 3.00   m sobre uma superfície horizontal até parar no ponto C .

(a) Qual é o coeficiente de atrito cinético entre o pacote e a superfície horizontal?

(b) Qual é o trabalho realizado pela força de atrito ao longo do arco circular do ponto A ao ponto B?

Passo 1

Falaaa, meu povo lindo!! Quais as novidades por aí? Por aqui, eu já tenho certeza que vamos sair craques nessa matéria com a resolução dessa questãozinha. Bora??

Um pacotinho é abandonado do repouso no início de um trilho ( A ) e desliza até parar no ponto C . Esse trilho é formado por uma parte que se assemelha a um quarto de circunferência e uma parte retilínea horizontal.

Bom a questão deseja que encontremos o coeficiente de atrito cinético entre o pacotinho e a superfície horizontal. Como podemos chegar a essa resposta???

Vamos utilizar a conservação de energia para a trajetória de B   até C :

E B   =   E C

K B +   U B +   W A t r i t o =   K C +   U C

Quando estamos calculando conservação de energia normalmente consideramos apenas a energia cinética ( K ) e a energia potencial ( U ) . Entretanto, temos nesse problema a força de atrito que retira energia do nosso sistema e para manter o sistema equilibrado é preciso adicionarmos o trabalho que foi dissipado por essa força.

Tomando a superfície horizontal como referência, temos que no ponto B e C a altura será zero. Devido a isso, a energia potencial ( U   =   m g h ) nesses pontos também será zero.

K B +   U B +   W A t r i t o =   K C +   U C

K B + 0   + W A t r i t o = K C + 0  

Como o pacotinho desliza até parar em C , podemos concluir que a energia cinética K C = 1 2 m v C ²   é igual a zero.

Logo,

K B   + W A t r i t o = K C  

K B   + W A t r i t o = 0  

  W A t r i t o =   - K B

W A t r i t o =   - 1 2 m v B ²

W A t r i t o =   - 1 2 m v B ²

E a fórmula do Trabalho, vocês lembram???

W   =   F ⋅ d ⋅ c o s ( θ )

Nesse caso a nossa força é a força de atrito!!! E vamos chamar de s a distância que o pacote percorre entre os pontos B e C. Então a equação fica assim:

F a t ⋅ s ⋅ c o s 180 ° =   - 1 2 m v B ²

Atenção! Não se esqueça que a força faz um ângulo de 180 ° com o deslocamento.

μ K ⋅ m g ⋅ s ⋅ c o s 180 ° =   - 1 2 m v B ²

μ K ⋅ m g ⋅ s ⋅ ( - 1 ) =   - 1 2 m v B ²

μ K ⋅ g ⋅ s = 1 2 v B ²

Substituindo com os valores em questão, temos que

μ K = ( 4.80   m / s ) ² 2 ( 9.8   m / s ² ) ( 3.00   m )

μ K = 0.392

Obaaa! Então, até aqui aplicamos um pouco de conservação de energia em um sistema com força de atrito (dissipativa) para descobrirmos o coeficiente de atrito cinético.

Bora para o segundo round !

Passo 2

Agora temos que encontrar o trabalho realizado pela força de atrito na primeira parte da trajetória, ou seja, na parte do trilho que se assemelha a um pedaço de circunferência.

Vamos utilizar novamente a conservação de energia só que agora para os pontos A   e B :

E A   =   E B

K A +   U A +   W A t r i t o =   K B +   U B

Como o objeto parte do repouso isso significa que a nossa energia cinética no ponto A é igual a zero. E no passo anterior, vimos que o B possui energia potencial U B   =   0 . Sendo assim,

0 +   U A +   W A t r i t o =   K B +   0

    W A t r i t o =   K B -   U A

Substituindo as fórmulas e lembrando que a altura do ponto A é igual ao raio da circunferência, temos que:

    W A t r i t o = 1 2 m v B ² - m g R

Substituindo com os dados do enunciado encontramos que:

    W A t r i t o = 1 2 ( 0.200   k g ) ( 4.8 m s ) ² - ( 0.200   k g ) ( 9.8 m s 2 ) ( 1.60   m )

    W A t r i t o = 2,304 - 3,136   k g ⋅ m 2 ⋅ s - 2

W A t r i t o =   - 0,82   J

Showw de bolinhas, utilizando novamente os conhecimentos de conservação de energia conseguimos descobrir o trabalho dissipado na primeira porção da trajetória.

Até mais galerinha! :)

Resposta

a) μ K = 0.392

b) W A t r i t o =   - 0,82   J

Exercícios de Livros Relacionados

Um escorrega de parquinho tem a forma de um arco de circunferência com 12m de raio . A altura do escorrega é h=4,0m e o chão é tangente à circunferência (Fig. 8-68). Uma criança de 25k g escorrega do
Um jogador de beisebol arremessa uma bola com uma velocidade inicial de 81,8m i / h . Imediatamente antes de outro jogador segurar a bola na mesma altura, sua velocidade é 110p é s / s é . De quanto é
Na Fig. 8-49, um bloco desliza para baixo em um plano inclinado. Enquanto se move do ponto A para o ponto B , que estão separados por uma distância de 5,0m , uma força F , com módulo de 2,0N e dirigid
Um operário empurra um caixote de 27k g , com velocidade constante, por 9,20m , ao longo de um piso plano, com uma força orientada 32 ° abaixo da horizontal. Se o coeficiente de atrito cinético entre
Uma criança que pesa 267N desce em um escorrega de 6 ,1m que faz um ângulo de 20 ° com a horizontal. O coeficiente de atrito cinético entre o escorrega e a criança é 0,10 . (a) Qual é a energia transf