Um bloco de massa é solto em repouso do alto de um plano inclinado de ângulo em relação ao plano horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância ao longo do plano, o bloco colide com uma mola de constante elástica , de massa desprezível, que se encontrava relaxada.
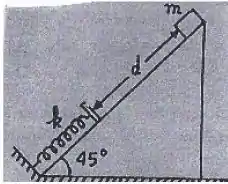
- Marque as forças atuantes sobre o bloco no momento da compressão. Calcule o trabalho realizado por cada uma das forças atuantes no problema desde o alto do plano até compressão máxima sofrida pela mola. Ache também o trabalho realizado pela força resultante.
- Ache a compressão sofrida pela mola para , , , e .
- Qual é a energia dissipada pelo atrito durante o trajeto máximo do bloco desde o alto do plano até compressão máxima sofrida pela mola?
- Após a compressão, a partícula retorna à sua posição de equilíbrio e liberta-se da mola, subindo ao longo do plano inclinado. Até que altura ela sobe?
Passo 1
a)
No momento da compressão as forças serão essas daí, saca só!
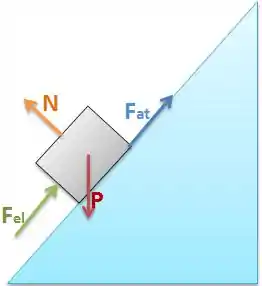
O trabalho da Força Peso será justamente . O nosso será a distância percorrida, somada à deformação da mola tudo multiplicado pelo , pois só queremos a variação de altura. Logo, teremos que:
O trabalho da Normal vai ser nulo, pois como o bloco percorre um caminho perpendicular a essa força, ao fazer o produto escalar, teremos:
O trabalho da Força de Atrito será dado por:
E o Trabalho da Força Elástica, como é de frenamento vai ser negativa, dada por simplesmente:
Passo 2
b)
Vamos utilizar a energia mecânica pra calcular isso aqui.
Utilizando como origem da referência do sistema o ponto mais baixo que a mola atingiu, teríamos que lá em cima do plano a energia mecânica total era:
E no final, no ponto mais baixo, a mola estará parada no ponto de origem do sistema e sua deformação será , logo a energia mecânica final será somente potencial elástica:
Logo
Substituindo
Como resolver isso aqui direto seria muuuuiiito chato, vamos substituir os valores numéricos do enunciado
Agora resolvendo essa equação por Bhaskara
Resolvendo a equação do segundo encontraremos que:
Como só nos interessa a solução com deformação positiva vamos ter
Passo 3
c)
Simples demais, é só tacar a fórmula que descobrimos no Passo 1.
Foram dissipados pela força de atrito.
Passo 4
d)
Calculando agora pelo Teorema Trabalho- Variação da Energia Cinética, teremos:
que é a energia cinética do bloco assim quando solto da mola, por sua vez é dada por:
O trabalho será dado por:
Substituindo toooooodos os valores, inclusive de da letra b, teremos que:
Resposta
a)
,
,
.
b)
c)
d)