UFSCAR, Sem Campus, Física 1, AV2 - 2021.1 - Prof° Raphael Santarelli, Questão 4d.
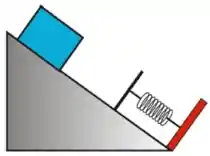
4) Um bloco de massa é solto, a partir do repouso, em um plano inclinado de em relação à horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava inicialmente relaxada, de acordo com o esquema mostrado na figura ao lado.
d) Se o coeficiente de atrito estático com o plano é de , o bloco continua parado ou começa a subir o plano inclinado depois de parar completamente?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
No item c) desse problema, vimos que a velocidade do bloco no instante que ele atinge a mola é de ou a partir daí, queremos calcular se, ao atingir a compressão máxima da mola, o bloco permanece parado ou se a mola empurra o bloco pra cima, dado que o coeficiente de atrito estático é dado por .
Mas então como fazemos para responder essa pergunta? 🤔
Nesse caso, podemos usar a regra de conservação de energia para energia não conservativas.
Não fez sentido nenhum, não é? 👀
A ideia é considerar a energia inicial do sistema, a energia final do sistema e a energia que é dissipada pelo atrito entre o bloco e o plano inclinado. Ou seja
Entendeu? Bora começar!
Passo 2
Inicialmente, quando o bloco encosta na mola, o bloco possui energia cinética já que o bloco está em movimento e também possui energia potencial gravitacional, já que após encostar na mola, o bloco ainda percorre uma distância .
A energia cinética é dada pela equação
Pelo enunciado, vimos que e vimos que , logo
Agora, a energia potencial gravitacional é dada como
Onde , e é a variação de altura que o bloco sofre ao comprimir a mola. Ou seja, ...
Tranquilo até aqui? 👍
Passo 3
No momento final, quando o bloco para devido a ação da mola, a energia o sistema vai ter, é dada pela energia que a mola aplica sobre o bloco e a energia que a força de atrito dissipa ao percorrer a distância .
A energia potencial elástica é dada pela equação
Se é a constante elástica da mola e é o valor que queremos encontrar, então
E a energia dissipada pelo atrito do bloco com o plano é dada pelo trabalho realizado pela força de atrito, ou seja, a força multiplicada pelo deslocamento
A força de atrito é dada por
Que por sua vez, a força normal é dada por
Substituindo tudo em , vamos obter
Substituindo , , e ...
Legal, né? 😁
Passo 4
Dessa forma, se a energia inicial é dada por
Já a energia final é dada por
E a energia dissipada é dada por
Portanto, substituindo esses resultados na equação que descrevemos no passo 1, temos
Calculando as raízes desse polinômio que obtemos que , no seu ponto de compressão é dado por
Está acompanhando? 👀
Passo 5
Por fim, para finalmente sabermos que a mola empurra o bloco para cima ou se o bloco permanece parado, temos que comparar a força que a mola faz no bloco com a soma da força de atrito estático que o bloco sofre ao ser empurrado e da força gravitacional que o bloco sofre.
O módulo da força de atrito estático é dado por
Já vimos que a força normal é dada por , portanto
Se o coeficiente de atrito estático é dado por , temos
Já o módulo da força que a mola faz no bloco é dado por
Se e , então
E por fim, o modulo da força gravitacional no sentido do movimento é dado pela lei do cosseno onde
Comparando as forças no ponto que que a mola está na sua compressão máxima, temos que se a força elástica for maior que a soma das forças gravitacionais e de atrito, o bloco sobe, caso o contrário, o bloco permanece parado
Vemos que , logo, o bloco sobe devido a ação da mola!
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
O bloco sobe devido a ação da mola!