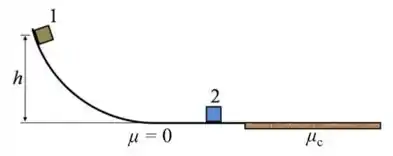
Questão 3). Na figura ao lado, o bloco , de massa , encontra-se inicialmente em repouso a uma altura , em uma pista sem atrito. O bloco é liberado e colide com o bloco , de massa , que estava inicialmente em repouso. Após a colisão, os blocos permanecem unidos e deslizam sobre a região com atrito e param depois de percorrerem uma distância . Sabendo que , determine o coeficiente de atrito cinético entre os blocos e o trecho com atrito. Os blocos são feitos do mesmo material. (Lembre-se que o coeficiente de atrito é uma grandeza adimensional)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nesse problema temos um bloco de massa no alto de uma rampa de altura . A rampa não possui atrito com o bloco e ao ser solto, o bloco escorrega até a base da rampa onde colide com outro bloco de massa .
Depois da colisão, os dois blocos ficam unidos e deslizam por cima de outra superfície que tem atrito cinético percorrendo uma distância até parar.
Se a distância é igual a qual é o valor do coeficiente de atrito cinético ?
Tem ideia de como fazer isso?? 🤔🤔
Para essa questão temos que ter em mente o conceito de conservação de energia e de momento linear.
Ta afiado nesse assunto? 😁
Se não tiver não tem problema!
O conceito de conservação de energia nos diz que se não há dissipação de energia como atrito por exemplo, a energia inicial do sistema é igual a energia final.
Mas quando temos alguma energia dissipativa a energia inicial é igual a energia final menos a energia dissipada.
Já o conceito de conservação do momento linear é bem parecido. Ele diz que o momento linear inicial é igual ao momento linear final.
Mas vamos com calma! Vamos começar do início.
Passo 2
Temos um bloco parado no topo de uma rampa sem atrito de altura , ou seja, nosso bloco possui energia potencial gravitacional nesse momento.
Que é dada pelo produto da massa · aceleração gravitacional · altura, ou seja
O bloco é solto e desliza sob a rampa até chegar à base.
Pelo princípio da conservação de energia (como não há energia dissipada), vemos que toda energia potencial se transforma em energia cinética.
Simplificando dos dois lados e isolando em um lado da igualdade, temos
Com isso vemos que a velocidade do bloco é ao chegar na base da rampa.
Entendeu essa parte? 😉
Passo 3
A segunda etapa desse problema diz que ao chegar na base da rampa, o bloco colide com o bloco que permanecem se movendo juntos.
Aqui entra o conceito da conservação do momento linear.
O momento linear é obtido pelo produto entre a massa do objeto e sua velocidade. Se o momento é conservado, então
Inicialmente o bloco , de massa , se movimenta com uma velocidade e o bloco , de massa está parado, ou seja
No fim, os dois blocos se juntam e passam a se movimentar a uma velocidade que vamos chamar de
Igualando os dois momentos, temos
Uhuul! Relacionamos as velocidades antes e depois da colisão. Agora vamos juntar isso no resultado que achamos no último passo.
Se calculamos anteriormente que , então
Simplificando dos dois lados e isolando em um lado da equação
Assim, vemos que imediatamente antes de mudar de superfície a velocidade dos blocos é da velocidade inicial do bloco .
Tranquilo até aqui? 👀
Passo 4
Nessa terceira etapa do problema, vamos considerar os blocos e como uma só, já que após a colisão os blocos se uniram.
Pelo princípio de conservação de energia quando há dissipação, temos que
Ou seja, a energia inicial é igual a energia final menos o trabalho realizado pela força dissipativa.
No caso a energia inicial é dada pela energia cinética dos blocos.
Simplificando a equação e se , então
Como e como , então
Simplificando um pouco mais, temos
Portanto a energia cinética inicial é dada por .
Interessante, não é? 😎
A energia final é , não é? Isso porque no fim os blocos estão parados, então a energia cinética é e como não há mudança de altura, a energia potencial também é .
Isso significa que toda a energia inicial é dissipada pelo atrito. Ou seja, a energia dissipada por atrito é igual a energia cinética que acabamos de calcular!
Tá mas quem é a força de atrito?
Passo 5
A força de atrito é dada por
Onde é a força normal dos blocos dada pelo produto entre a massa e a aceleração gravitacional
Portanto a força de atrito é dada por
Mas como a massa do nosso conjunto agora é , então
Podemos obter a energia dissipada por essa força calculando o trabalho realizado por essa força.
O trabalho de uma força é obtido pelo produto entre ela mesma e a distância percorrida, no nosso caso será
No enunciado foi dito que , ou seja, , fazendo essa substituição em , temos
Estamos chegando na reta final! 😁
Bora lá!
Passo 6
Substituindo as energias que calculamos em , temos
Simplificando os dois lados cortando , e , temos
Isolando em um lado da equação, vamos obter
No fim do problema foi dito “Lembre-se que o coeficiente de atrito é uma grandeza adimensional”
Perceba que o resultado que obtemos independe de qualquer grandeza, ou seja, é adimensional! Isso valida nossa resposta.
Então o coeficiente de atrito cinético entre os blocos e a superfície é .
É isso! Essa resolução te ajudou? Responde Aí! ✌
