Considere um plano inclinado que forma um ângulo de o com a horizontal. Na parte inferior do plano inclinado está uma mola com constante elástica de fixada num muro. Um bloco de inércia solto na parte superior do plano inclinado produz uma compressão máxima na mola de em relação à posição inicial

a) Desprezando todos os atritos calcule a distância que o bloco percorre desde o momento em que é solto até comprimir a mola no seu valor máximo.
b) Agora considere que existe atrito entre a superfície do bloco e o plano inclinado com . Calcule a distância em que o bloco foi solto para comprimir a mola do mesmo valor máximo anterior.
c) Qual a aceleração do bloco ao descer a rampa com atrito?
d) Se você quiser que o bloco desça com velocidade constante a rampa com atrito qual o ângulo a rampa dever ter com a horizontal
Passo 1
a) Vamos começar!
Bem! Nesse primeiro item, temos que calcular a distância que o bloco percorre desde o momento em que é solto até comprimir a mola no seu valor máximo.
Essa é de boas! Bastar usar a conservação da energia...
Substituindo os valores numéricos...
E a distância percorrida pelo bloco referente a essa altura é a hipotenusa da rampa, igual à...
Somando com a compressão máxima, podemos obter a distância total...
Passo 2
b) Agora, vamos ver no caso em que há atrito! Sabemos que o coeficiente de atrito vale
Sendo assim, uma vez que o trabalho de forças não conservativas é igual à variação de energia mecânica, temos que...
Onde vai ser a distância total percorrida pela bloco...
Passo 3
c) Agora, vamos fazer a decomposição de forças na rampa, considerando que há atrito...
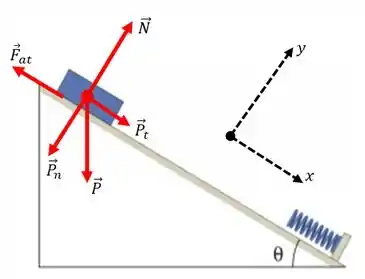
Com base nisso, aplicando o somatório das forças podemos descobrir o que pede esse item, que é a aceleração do bloco quando há atrito...
Passo 4
d) E pra finalizar, falta descobrir o ângulo para o qual o bloco vai descer sem aceleração, com velocidade constante...
Ora bolas! Pois muito bem! Aplicando o somatório das forças na direção :
Resposta
a)
b)
c)
d)