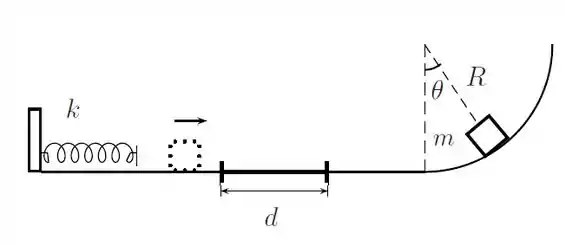
Um pequeno bloco de massa , após ser empurrado a partir do repouso por uma mola de constante elástica , comprimidade uma distância , desliza sobre uma superfície horizontal. Após se soltar da mola, ele passa por um trecho de comprimento , única região em que o atrito não é desprezível e cujo coeficiente de atrito cinético é . No final desta superfície horizontal, o bloco começa a subir uma rampa vertical semicircular de raio . Uma vez na rampa o bloco atinge uma posição, cuja direção faz um ângulo , desconhecido, com a vertical, onde para momentaneamente e volta descendo a rampa; como mostra a figura. Calcule
a) a velocidade do bloco imediatamente antes de começar a subir a rampa semicircular;
b) o ângulo alcançado;
c) o módulo da força normal, ao atingir o ângulo . Apresenta a resposta em função dos dados do problema e do ângulo ;
d) o módulo da velocidade máxima do bloco durante o seu movimento e onde ela ocorre; justifique sua resposta.
Passo 1
a) Vamos utilizar aqui o princípio da conservação da energia mecânica, no entanto, ele vai ter uma variação! Você viu que a superfície possui atrito? Portanto a variação da energia mecânica será igual ao trabalho da força de atrito, beleza?
Como temos somente energia cinética e potencial elástica nesse trecho do percurso, temos:
Onde:
E:
Portanto:
Logo:
Passo 2
b) Agora não há mais atrito e podemos usar a conservação de energia direto!
Substituindo que encontramos na letra (a):
Analisando a geometria do problema:
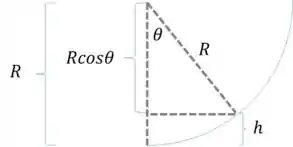
Vemos então que:
Logo:
Substituindo o :
Passo 3
c) Em um movimento circular, sabemos que a resultante das forças que apontam pro centro é igual a força centrípeta, logo:
Sabemos então que:
Como a velocidade neste ponto é nula:
=
Passo 4
d) A região em que a velocidade é máxima é entre o ponto em que o bloco solta da mola até o ponto onde começa o atrito, já que toda a energia elástica foi convertida em cinética e esta ainda não foi reduzida pelo atrito, certo? Portanto:
Resposta
a)
b)
c)
d)