Uma corda é usada para puxar um bloco de massa com velocidade constante ao longo de uma superfície horizontal com atrito. A força constante que a corda exerce no bloco possui módulo e direção formando um ângulo com a horizontal (ver figura a seguir). O bloco se desloca horizontalmente.
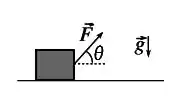
Calcule:
(a) o trabalho desta força ao longo de um deslocamento de comprimento do bloco;
(b) o coeficiente de atrito cinético entre o bloco e a superfície horizontal;
(c) o trabalho da força de atrito ao longo deste deslocamento . Se a força é conservativa, de quanto variou a sua energia potencial neste deslocamento?
Passo 1
a) Como a força é constante ao longo do percurso:
Passo 2
b) Foi dito que a velocidade do bloco é constante, portanto:
Usando a segunda Lei de Newton, primeiramente no eixo :
Para o eixo :
Substituindo o valor da normal na equação anterior:
Passo 3
c) O trabalho da força de atrito pode ser calculado como:
Como a força é conservativa, podemos usar que:
Portanto:
Resposta
a)
b)
c)