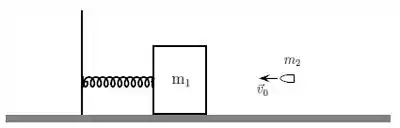
Um bloco de madeira de massa está inicialmente em repouso sobre uma superfície horizontal de atrito desprezível. Uma mola ideal tem uma de suas extremidades ligada ao bloco enquanto a outra extremidade está ligada a uma parede. Inicialmente a mola não está distendida nem comprimida. Uma bala de massa , com velocidade horizontal de módulo , atinge o bloco e nele fica alojada, fazendo com que a mola seja comprimida de uma distância .

a) Qual o módulo da velocidade do bloco imediatamente após ser atingido pela bala?

b) Qual a constante elástica da mola?

c) Supondo agora que exista atrito entre o bloco e o chão com um coeficiente de atrito cinético entre as superfícies . Calcule qual deve ser a constante elástica de uma outra mola que substituiu a primeira para que a compressão máxima da mola continue sendo .

Aplicando a conservação do momento linear:

Inicialmente, temos apenas a bala em movimento:

Enquanto no final, temos que o conjunto do bloco com a bala saem juntos com uma mesma velocidade :

Juntando tudo na equação da conservação, temos:

Na letra (b), queremos a constante elástica da mola .

Temos como dado a deformação da mola .

Como a força da mola varia à todo instante com a sua deformação, resolver esse problema por cinemática ficaria mais difícil.

Então, um bom caminho aqui é resolver por energia.

A única força que vai atuar durante o movimento após a colisão é a força elástica.

Como a força elástica, assim como a força peso, não alteram a energia total do sistema (forças conservativas), temos a conservação da energia mecânica:

A energia mecânica é a soma da energia cinética com a energia potecial :

Logo após a colisão, a mola ainda não está deformada e por isso ão há energia na forma de potencial elástica. Toda a energia está na forma de energia cinética.

Enquanto na situação onde a mola chegou em sua compressão máxima e o sistema parou, toda a energia está na forma de potencial elástica e não sobra nenhuma parcela na forma de energia cinética:

A energia cinética é dada por:

Então, na situação inicial, temos:

Substituindo a expressão para que achamos no PASSO 2:

Já aa energia potencial elástica é dada por:

Na situação final, temos que a deformação da mola foi de :

Juntando as expressões, temos:

Isolando , ficamos com:

Já na letra (c), a situação muda um pouco.

Como temos atrito, o sistema iria dissipar energia ao longo do deslocamento, fazendo o bloco parar antes da situação da letra (b).

Então, para que o bloco consiga ter o mesmo deslocamento que antes, precisamos colocar uma nova mola de constante elástica .

Queremos descobrir esse .

Como temos atrito atuando, a energia mecânica não se conserva mais...

Então, podemos utilizar qualquer uma das duas expressões:

O teorema trabalho-energia cinética:

Ou então, que a variação da energia mecânica é o trabalho das forças não conservativas:

Vamos usar a segunda.

Nesse caso, a única força não conservativa atuando é a força de atrito, então:

A energia mecânica inicial estará toda na forma de energia cinética, igual ao que já fizemos para a letra (b):

Já a energia mecânica final estará toda na forma de energia potencial elástica:

Sendo que a nova constante elástica da mola é e a deformação é a mesma :

Por último, vamos calcular o trabalho da força de atrito nesse deslocamento .

O trabalho da força de atrito é dado pelo produto escalar entre a força e o deslocamento:

Como a força de atrito está contrária ao deslocamento, temos:

A força de atrito é dada por enquanto o deslocamento do bloco será a mesma distância que a deformação da mola :

Além disso, temos que a força normal está em equilíbrio com a força peso do bloco e da bala (na vertical), assim a força normal será:

Temos:

Juntando todas as expressões na equação de energia, ficamos com:

Isolando , temos:

Pronto, chegamos na resposta apenas em função dos parâmetros conhecidos.

Podemos ainda deixar a resposta mais bonitinha...

Repare que o primeiro termo é exatamente igual a :

Então, ficamos com: