UFABC – Fenômenos Mecânicos – Lista 4 – Questão 12
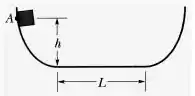
Uma partícula pode deslizar em uma pista com extremidades elevadas e uma parte central plana, conforme mostrado na figura. A parte plana tem um comprimento . Os trechos curvos da pista não possuem atrito, mas na parte plana o coeficiente de atrito cinético vale . A partícula é solta a partir do repouso no ponto , que está a uma altura . A que distância da borda esquerda da parte plana a partícula finalmente para?
Passo 1
Oi, tudo bom? Essa questão parece complicada, mas vou ajudar você!
Temos que na posição inicial (no ponto A) a partícula está em repouso, logo possui apenas energia potencial.
Conforme ela desliza, ela vai perdendo energia potencial e ganhando energia cinética, ao chegar no plano temos a perda de velocidade pelo atrito.
Com isso, temos que o trabalho realizado é
No início e no fim do movimento, a energia cinética é zero e como não há forças externas . A energia mecânica então envolve apenas a energia potencial gravitacional.
Tomando a base da rampa com referencial para energia potencial gravitacional
Passo 2
Não sabemos em quantas voltas o bloco irá parar, mas temos ideia de que ele irá parar na região plana. Caso seja na primeira volta
Com . Se for na segunda volta
Com . E assim por diante. Generalizando para a enésima volta
Para
Assim teremos
Sendo
Para
Para
Tranquilo?
Passo 3
Para que , , logo
Para
Beleza?
E é isso! Então o bloco para a da extremidade esquerda (e após a terceira volta).
Espero ter ajudado!