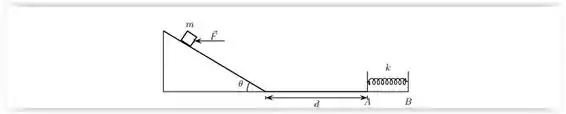
Um bloco de massa m desce acelerado ao longo de uma rampa inclinada de um angulo em relação à horizontal, como indicado na figura. Um dispositivo exerce sobre o bloco uma força constante horizontal, como indicado na figura. O coeficiente de atrito cinético entre a superfície do plano inclinado e o bloco vale µ. Ao atingir a base do plano inclinado, o bloco tem uma velocidade e o dispositivo que exerce a força é desligado. O bloco percorrerá uma distância sobre uma superfície horizontal, com o mesmo coeficiente de atrito µ até encontrar a extremidade de uma mola de constante elástica k, fixa na outra extremidade. Considere desprezível o atrito na região A-B. (Todas as respostas devem ser dadas em termos de m, , F, µ, g, k, v0 e d)
- represente e identifique todas as forças que agem sobre o bloco enquanto ele esta sobre o plano inclinado;
- determine o modulo da aceleração com que o bloco desce o plano;
- calcule a compressao máxima da mola.
Passo 1
Primeiramente, vamos entender as forças que agem sobre o bloco quando ele está no plano inclinado.
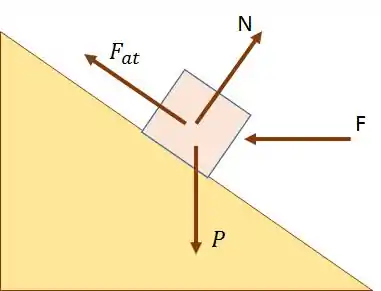
é a força de atrito
é a normal
é a força constante horizontal
é a força peso
Passo 2
Para acharmos o módulo da aceleração que o bloco desce, vamos aplicar a segunda lei de newton:
No caso do problema:
Para achar a decomposição das forças, vamos colocar os eixos na direção de queda do bloco e na direção ortogonal à rampa, na seguinte forma:
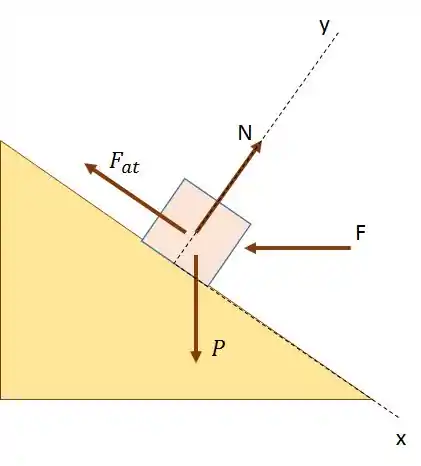
A partir disso, podemos montar a equação:
Lembrando que î é o vetor unitário na direção do eixo x e j é o vetor unitário na direção do eixo y. Podemos reparar, também, que só há aceleração na direção î.
Passo 3
A partir da equação montada acima, podemos separar em eixo x e eixo y.
Dessa forma montamos:
Eixo x:
Eixo y:
Show! E agora?
Precisamos lembrar da relação entre normal e força de atrito cinético: .
Aplicando na equação do eixo do problema, chegamos a:
Após isso, podemos substituir na equação do eixo x:
Pronto!
Precisamos só ajeitar isso aí!
Passo 4
Como temos a presença de uma força não conservativa de atrito vamos usar o teorema trabalho-energia cinética.
Repare que depois que o bloco desce do plano inclinado, a única força que realiza trabalho é a , o dissipando. Logo, usaremos o sinal negativo. Como sabemos a distância percorrida, podemos tirar o valor do trabalho realizado pelo atrito.
Aplicando isso para a situação do problema, teremos:
Mas, precisamos manipular isso ainda.
Lembra que aplicamos na letra b que ?
Depois que o bloco desce do plano inclinado e faz seu trajeto em linha reta, a normal vale .
Assim,
Substituindo isso na equação do Teorema trabalho- energia cinética, chegamos a:
Manipulando, chegamos ao valor de .
Passo 5
Bom, já sabemos qual é a velocidade que o bloco chega depois de percorrer a distância d. Mas o problema pede a compressão da mola.
Como vamos relacionar isso?
A sacada aqui está em reparar que ao longo da região AB não existem forças que realizam trabalho e que não há mudança de altura, ou seja, não há energia potencial gravitacional.
Podemos aplicar a conservação de energia mecânica, já que no momento de compressão máxima da mola toda energia cinética do bloco que encontra a mola se transforma em energia potencial elástica.
Substituindo pelo que achamos no Passo 4:
- '' - '' - '' - ''Resposta
a)
b)
c)