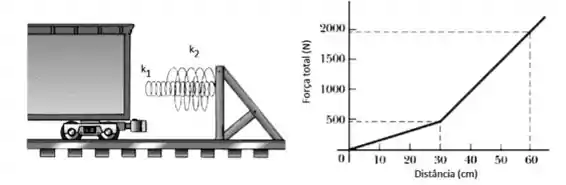
Um vagão de carga com se desloca ao longo de trilhos horizontais com atrito desprezível e velocidade constante. O vagão é parado por uma combinação de duas molas em espiral, como ilustra a figura. As duas molas obedecem à lei de Hooke e suas constantes elásticas valem e . Após a primeira mola ser comprimida por uma distância , a segunda mola passa a agir juntamente com a primeira para aumentar a intensidade da força aplicada ao vagão. A força do conjunto é mostrada no gráfico abaixo. O vagão é parado a uma distância após o contato com a primeira mola. Todas as respostas devem ser fornecidas utilizando APENAS considerações sobre o trabalho realizado por uma força e o teorema do trabalho – energia cinética. Todos os cálculos devem ser justificados.
(a) Calcule qual é o trabalho realizado por cada uma das forças que atua sobre o vagão durante sua frenagem.
(b) Calcule qual é o módulo da velocidade do vagão logo antes dele encostar na primeira mola.
(c) Suponha agora que uma força de atrito atue entre os trilhos e o vagão e que o mesmo possua velocidade logo antes dele entrar em contato com a primeira mola. Se o vagão para a uma distância após o contato com a primeira mola, calcule o valor do coeficiente de atrito cinético entre os trilhos e o vagão.
Passo 1
(a)O trabalho realizado pela força peso é dado por:
Já pela normal é:
E finalmente, o trabalho da força elástica é:
Os valores das forças elásticas em e referentes ao gráfico valem:
Somando então a área do triângulo até com a do outro triângulo de até :
Passo 2
Pela conservação da energia, temos:
Substituindo os valores:
Passo 3
(c) Para este item, basta adicionarmos o trabalho da força de atrito na conservação de energia:
Substituindo a equação da força de atrito:
Resposta
a) ; ;
b)
c)