UFSCAR, Sem Campus, Física 1, AV2 - 2021.1 - Prof° Raphael Santarelli, Questão 4c.
4) Um bloco de massa é solto, a partir do repouso, em um plano inclinado de em relação à horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava inicialmente relaxada, de acordo com o esquema mostrado na figura ao lado.
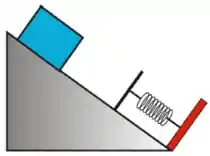
c) Qual a velocidade do bloco no momento em que entra em contato com a mola?
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema, temos que obter a velocidade de um bloco, partindo do repouso, no instante em que ele colide com a mola que está na base do plano inclinado.
Tem alguma ideia do que podemos fazer? 🤔
Primeiro, temos que evidenciar algumas informações importantes!
A massa do bloco é , o ângulo que o plano faz com a horizontal é , o coeficiente de atrito cinético entre o bloco e o plano é de e a distância que o bloco percorre até encostar na mola é igual a .
Para resolver esse problema, podemos aplicar a lei da conservação de energia, ou pelo menos uma análoga a isso, já que o bloco possui atrito com o plano.
Ou seja
Sacou, bora analisar cada fase separadamente! 😉
Passo 2
Primeiro vamos analisar no momento inicial, as energias que temos no sistema.
O bloco parte do repouso, portanto a energia cinética é e consequentemente as perdas com a força de atrito é .
O bloco vai cair de uma certa diferença de altura, logo, inicialmente o bloco possui um potencial gravitacional.
Essa última energia pode ser calculada como
No enunciado, vemos que e foi pedido para considerarmos . Já deve ser calculado como a diferença de altura que o bloco percorre até o ponto em que encosta na mola.
Como a superfície que o bloco percorre é dado por e o ângulo que a superfície faz com a horizontal é , podemos obter a partir de um triangulo retângulo.
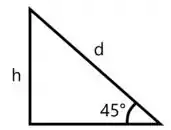
Pela lei dos senos, temos que
dessa forma, a energia inicial do sistema é dada por
Tranquilo até aqui? 😁
Passo 3
Para obter a energia mecânica final e a energia dissipada pela força de atrito, calculamos a energia cinética final como se não houvesse atrito, porém sem saber a velocidade final, e a energia dissipada é obtida calculando o trabalho realizado pela força de atrito.
A energia cinética em um instante é dada por
é o que queremos encontrar e sabemos que é , logo
Já o trabalho realizado por uma força é dado por
No caso, a força é igual a força de atrito , ou seja
E é a força normal à superfície, dada por
Ou seja
Substituindo em ...
Substituindo as variáveis em , vamos obter
Legal, né? 🤩
Passo 4
No passo 1, definimos que a equação que rege nosso problema é dada por
Vimos que inicialmente a bloco possuía apenas energia potencial gravitacional, ou seja
No instante em que o bloco encosta na mola, após percorrer uma distância a energia mecânica final foi dada pela energia cinética do bloco, ou seja
E por fim, as perdas de energia que acontecem no sistema é em decorrência à força de atrito, assim, a energia que é desperdiçada é dada pelo trabalho que essa força realizou, ou seja
Substituindo esses valores na equação do passo 1, temos
Isolando a velocidade ...
Simplificando...
E essa é a velocidade do bloco no instante em que ele toca a mola é igual a, aproximadamente, !
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
