Um elevador de massa está em repouso a uma altura de , medida a partir do fundo do poço, quando o seu cabo rompe. O dispositivo de segurança do elevador é ativado de forma instantânea, mas não funciona corretamente. O elevador então inicia um movimento de descida lenta deslizando sobre trilhos laterais os quais geram uma força de atrito intensa e constante igual a . No fundo do poço há uma mola de comprimento igual a (quando relaxada), que vai auxiliar o trilho a parar o elevador. A constante elástica da mola é desconhecida. Depois da mola ser comprimida de o elevador entra em repouso. Utilize para a aceleração da gravidade. Suponha a origem do potencial como sendo o fundo do poço.

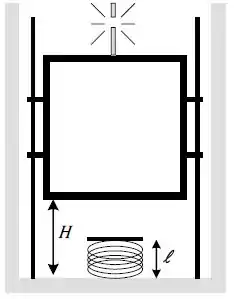
a) Determine a energia cinética do elevador na iminência de encostar na mola, em função dos dados do problema.

b) Assumindo que a energia cinética do elevador na iminência de encostar na mola é , determine a energia máxima armazenada na mola, em função dos dados do problema.

c) Utilize somente para este item os seguintes dados numéricos: , , , , 𝑒 . Calcule a energia potencial gravitacional do elevador quando ele estiver em repouso na posição do item b).

Vamos estabelecer cada um desses caras.

No início, o elevador está em repouso, então temos apenas energia potencial gravitacional :

Quando o elevador encosta na mola, ele tem uma energia cinética associada a sua velocidade e uma energia potencial gravitacional , relacionada a sua altura:

Como a altura que o elevador se encotra será a altura da mola relaxada, temos:

Por último, temos .

Como a força de atrito age contra o deslocamento, seu trabalho será negativo:

O deslocamento é a diferença da altura inicial para a altura da mola :

Voltando à equação de energia:

Isolando , temos:

Na letra (b), queremos a energia máxima armazenada na mola.

A energia armazenada em uma mola é dada por:

Então, a energia é máxima quando a deformação for máxima.

A compressão máxima ocorre no momento em que o elevador para.

O enunciado já deu a deformação máxima da mola , porém, não temos a constante da mola como dado, então vamos recorrer novamente à equação de energia.

Como a questão forneceu como dado a energia cinética no ponto em que o elevador toca a mola, vamos escrever a equação de energia entre esse ponto e o ponto em que o elevador para.

Já calculamos, no item (a), a energia no ponto em que o elevador toca a mola. Então a energia será:

Mas, agora, a energia cinética é um valor conhecido , dado no item (b):

Vamos à energia final ...

A energia final será apenas as energias potenciais gravitacional e elástica:

Como a mola deforma , a altura final do elevador será:

Então temos:

Já o trabalho da força de atrito será a partir do deslocamento (o quanto a mola deformou):

Juntando tudo isso, temos:

Isolando :

Podemos colocar em evidência o , mas só para ficar mais bonitinho mesmo:

Na letra (c), queremos o valor numérico da energia potencial gravitacional do elevador quando ele estiver parado.

Já vimos na letra (b) que a energia potencial gravitacional nessa posição é:

Tá vendo esse monte de dado numérico fornecido pela questão?

É, só vamos precisar de , e mesmo. O resto é para confundir a gente.

Os valores numéricos estão em unidades bem diferentes, para padronizá-los, vamos jogar no SI:

A massa está em toneladas:

O comprimento da mola está em centímetros:

Substituindo os valores numéricos, temos: