Um bloco é liberado a partir do repouso conforme a figura abaixo, iniciando seu movimento a partir da extremidade esquerda da figura. Os trechos em rampa não possuem atrito, e os trechos planos possuem atrito, com coeficiente de atrito cinético de . O valor de .
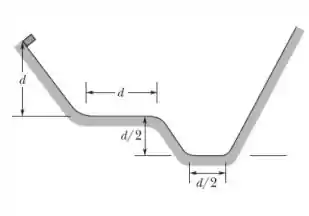
Após atingir essa altura máxima na rampa da direita, o bloco inicia o movimento contrário, se movendo agora da direita para a esquerda. Com que velocidade o bloco atinge o final do primeiro trecho plano (mais baixo)? Com que velocidade o bloco atinge o início do segundo trecho plano (mais alto)? Qual a posição exata em que o bloco para totalmente?
Passo 1
Oiie, tudo bem?
Temos nesta questão uma rampa formada por diversos trechos de comprimentos e alturas diferentes! Em particular temos três trechos e eles estão distribuídos como na seguinte imagem
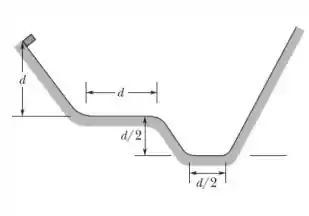
note que . Nós agora temos que analisar o caminho contrário ao da alternativa anterior, ou seja, após chegar a uma altura máxima, que encontramos na alternativa anterior como
iremos obter as velocidades no final do trecho plano mais baixo, a velocidade no início do trecho plano mais alto, e verificar onde o bloco irá parar depois do atrito ter consumido toda a energia cinética! Eu vou repetir ao longo dos passos as expressões para as energias cinéticas e para o trabalho da força de atrito, mas vale a pena utilizar os resultados obtidos para os atritos realizados no trecho plano mais baixo
e, no trecho plano mais alto
Com tudo isso em mãos! Vamos resolver esta questão! Vem comigo!
Passo 2
Primeiro, as duas equações que serão úteis para nós aqui são, a expressão para a energia potencial gravitacional
em que é a massa do bloco (irrelevante para nós aqui), é a aceleração gravitacional e é a altura em um referencial de nossa escolha! Também iremos precisar da expressão para a energia cinética
em que é o módulo da velocidade que o bloco tem em algum instante específico desejado. Vamos usar também o trabalho realizado pela força de atrito
em que é o módulo da força normal atuando sobre a partícula. Como só temos atrito nas seções planas, temos que a força normal será sempre igual em módulo ao peso do bloco, ou seja
e, o trabalho da força de atrito será sempre
em que é o deslocamento do bloco na região com atrito! Maravilha! Vamos aplicar estas expressões! Saca só!
Passo 3
Inicialmente o corpo está em uma altura máxima que encontramos no fim da alternativa anterior, e portanto, tem a seguinte energia potencial
como não há atrito nas rampas, temos que esta energia se transforma totalmente em energia cinética, temos que
Mas, esta é a energia cinética no início do trecho plano mais baixo, queremos no final do trecho plano mais baixo, ou seja, precisamos considerar a influência do atrito para percorrer a distância de . Como calculamos na alternativa anterior, temos que este atrito é dado por
e, portanto, a energia cinética é reduzida nesta quantidade, temos que a energia cinética restante será
Podemos calcular a velocidade ao final deste trecho usando a definição da energia cinética e substituindo os valores
ou simplesmente
que é aproximadamente
Agora, vamos ver quanta dessa energia cinética é necessária para subir a segunda rampa! Saca só!
Passo 4
Para subir toda a rampa é necessário que a energia cinética seja maior (ou ao menos igual) a energia potencial necessária para chegar a altura , temos que esta energia potencial é tal que
Inicialmente, temos uma energia cinética dada por
A energia cinética que irá restar no topo desta rampa é
Portanto, temos que a velocidade no topo da rampa será
Isolando a velocidade, temos que
ou, simplesmente
Ótimo! A última coisa que eles nos pedem é para analisar onde o bloco irá parar! Eu tenho um instinto que talvez ele pare neste trecho plano, mas claro, precisamos checar isso! Como fazemos isso? Saca só!
Passo 5
Para saber se o bloco irá parar neste trecho plano precisamos ver se a energia cinética relacionada a velocidade é maior do que o trabalho realizado pelo atrito ao longo de todo o trecho, nós calculamos este trabalho na alternativa anterior como
Vamos dar um valor qualquer para a massa aqui, já que ela é um fator comum no trabalho e na energia cinética, apenas para conseguirmos comparar as duas relações, colocando , temos que
A energia cinética se temos , será
Ou seja, a energia não é o suficiente para chegar ao final do trecho! O bloco irá parar antes de chegarmos à rampa! Vamos ver exatamente onde! Bora lá!
Passo 6
A energia cinética será toda eliminada na forma de trabalho pela força de atrito, ou seja, temos que
usando a definição de trabalho para a força de atrito, temos em módulo que
Então quanto deslocamento o bloco conseguirá fazer? Isolando temos que
ou, jogando em uma calculadora, temos que
Sendo assim, o bloco irá parar a esquerda do final do trecho plano mais alto! Uff… A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
, e à esquerda do final do trecho plano mais alto!