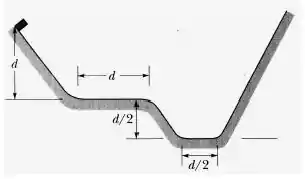
Passo 1
Oi, galerinha! Tudo bom? Essa questão parece complicada, mas vou decifrar ela pra você!

Nessa questão vamos usar a conservação da energia e analisar cada treixo do caminho, vamos começar?

Beleza?
Passo 2
Do começo ao final do plano, temos perda de energia cinética devido ao atrito

Como vimos na equação 1 que a energia cinética será igual a potencial, temos, a energia cinética com que o bloco chega ao final desse primeiro platô:
Como,
E como
Beleza? Essa é a energia com que o bloco chega ao final o primeiro platô, vamos agora analisar o que acontece com ele na segunda rampa!

Passo 3
Beleza? Essa é a energia cinética com que o bloco chega ao segundo platô! Nesse platô ele vai perder energia por causa do atrito!

Mas calma! Estamos quase no fim do percurso!
Passo 4
![]()
Como novamente:
Beleza? Então essa é a energia cinética que o bloco chega ao final desse segundo platô e segue rumo à terceira rampa!

Passo 5
Estamos interessados em saber onde o bloco para na rampa. Nesse instante, toda a energia cinética será transformada em energia potencial gravitacional, logo
E lembrando que , assim podemos calcular a altura com que o bloco para momentaneamente :
Ufa! Terminamos!

O bloco alcança então a terceira rampa e para em .
É isso! Espero ter ajudado!
Resposta
O bloco alcança a rampa e para quando .