UFF, Física 1, Prova 2, 2016.1
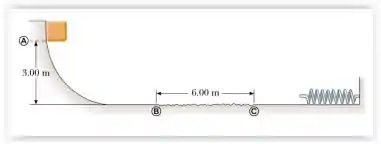
Um bloco com massa m = 10,0 kg é solto do repouso do ponto A da figura. O pavimento é sem atrito, exceto pelo trecho entre os pontos B e C, o qual tem comprimento 6,00 m. O bloco então atinge a mola, cuja constante elástica é k = 2250 N/m, e a comprime 0,300 m a partir da sua posição de equilíbrio. Qual o coeficiente de atrito cinético entre o bloco e o pavimento entre os pontos B e C?
(A) µc = 0,328
(B) µc = 0,432
(C) µc = 0,278
(D) µc = 0,156
(E) µc = 0,500
Passo 1
Vamos entender o problema. De início, quando não tem atrito, a energia mecânica é conservada. Do ponto B ao ponto C, o trabalho do atrito é dissipador, ou seja, impede que a energia mecânica se conserve. Nesse caso, qual é o melhor caminho?
Vamos descobrir qual era a energia mecânica inicial, qual foi a final e, pela diferença das duas, descobriremos o trabalho do atrito. Vamos lá?
Assim, o trabalho de atrito (causa dessa perda de energia) é igual a:
Passo 2
Bom, agora precisamos descobrir . Para isso, vamos usar a equação do trabalho do atrito e a relação entre força de atrito, coeficiente e normal.
Assim, montamos:
Como o plano de B até C não é inclinado, podemos dizer que:
Assim, montamos novamente:
Resposta
(A) µc = 0,328