UFSCAR; Física 1; AV2 - 2021.1 - Prof° Raphael Santarelli; questão 4a
Um bloco de massa é solto, a partir do repouso, em um plano inclinado de em relação à horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância de ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava inicialmente relaxada, de acordo com o esquema mostrado na figura ao lado.
a) Qual é a compressão sofrida pela mola?
Passo 1
Oi oi galerinha, por aí tá tudo certo??
Vamos começar traduzinho esse enunciado aí hein! Vem comigoo!
O enunciado nos diz que um bloco de massa deslizou uma distância em um plano inclinado de , até encontrar uma mola de constante de , considerando que o bloco atritou com coeficiente de atrito cinético de . Não conseguiu imaginar? Olha o desenho do nosso probleminha...
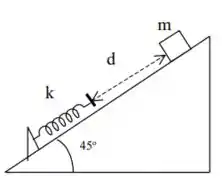
Nossa missão vai ser determinar quando a mola é comprimida à medida que o bloco desliza para baixo!
Passo 2
O segredo aqui vai ser determinar a energia mecânica no início da compressão, beleza? Então, para simplificar o problema, vamos dividir em duas partes!
Antes do bloco atingir a mola:
Aqui a energia mecânica inicial é perdida em parte devido ao atrito, colocando isso em uma fórmula, teremos:
Sabendo que o trabalho do atrito é dissipativo e, portanto, deve ser representado com sinal negativo na equação. Assim, a energia mecânica que antes era apenar gravitacional, passa a ser escrita como:
Como , podemos substituir na equação e fazer a famosa simplificada pra facilitar nossa vida!
Agora, substituindo apenas os valores dados no enunciado, teremos que a energia final equivale a:
Passo 3
A segunda parte é,
Após atingir a mola:
Aqui a variação de energia mecânica da nossa massa ocorrerá devido ao atrito e À transferência de energia para a mola se comprimir, show? Então temos
Nós vamos ter que ter um pouquinho de maldade pra não cair na pegadinha nesse passo, pois nessa etapa a energia mecânica final é só energia potencial gravitacional, já que queremos a compressão máxima da mola, ou seja, quando a velocidade do bloquinho chegar a 0 e .
Para não confundirmos, vamos pensar agora que na posição de equilíbrio da mola o potencial gravitacional é 0, então se o bloquinho desceu uma altura de h até a compressão toda da mola seu deslocamento foi de –h.
Portanto, a variação de energia mecânica é
Usando a mesma relação entre altura e deslocamento x no plano temos
Além disso, o resto da equação (1) ficaria da seguinte forma:
Teremos:
Podemos reescrevermos formato equação do segundo grau
Substituindo na equação para achar as raízes.