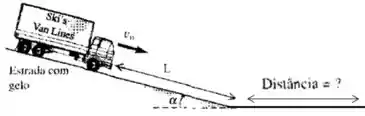
O freio de um caminhão de massa deixa de funcionar quando ele está descendo uma estrada de montanha com gelo inclinada de um ângulo . Inicialmente o caminhão desce a montanha com velocidade . Depois de percorrer, com atrito desprezível, uma distância até a base da montanha, o motorista vira o voltante e faz o caminhão seguir por uma estrada de emergência para caminhões. A estrada para caminhões é pavimentada com areia fofa que possui um atrito de rolamento igual a . Qual é à distância percorrida pelo caminhão desde a rampa até parar? Use o método da energia.
Passo 1
Vamos seguir a recomendação do enunciado e usar o método da energia.
Antes, vamos escrever os dados do problema
Ele quer a distância percorrida (vamos chamá-la de ), mas lembre-se ela não é dada.
A única força não conservativa q temos é a
Como o corpo está parado, e está no chão
Temos então
Devemos encontrar cada energia e o trabalho da força de atrito
Passo 2
Vamos achar as energias primeiro,
Passo 3
Repare que não temos a altura do caminhão, porém temos
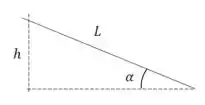
Então, vamos “decompor”
Então
Passo 4
Vamos agora achar o trabalho da , para isso devemos achar primeiro o seu módulo
Para encontrarmos , vamos usar sua fórmula
Nessa região a normal será igual ao peso (não estamos mais no plano inclinado)
Passo 5
Para encontrarmos seu trabalho
Isso porque a força está no sentido contrário ao deslocamento.
Então
Passo 6
Recapitulando
Queremos resolver
Tendo
Substituindo teremos
Beleza, então achamos a distância , que é quanto o caminhou andou na parte reta. Mas, notem que a questão pede a distância total que o camihão andou desde a rampa até parar. Então, a distância total, , vai ser a distância da rampa, , mais a parte reta, .