Dois objetos A e B de massas M e 2 M , respectivamente, são deslocados de uma distância d ao longo de um plano inclinado por uma força F paralela ao plano . O coeficiente de atrito cinético entre as superfícies de cada objeto e a do plano inclinado tem o mesmo valor c. No ponto mais alto, pode-se afirmar que
(A)
(B)
(C)
(D) O trabalho realizado por sobre o corpo A é maior do que o trabalho realizado por sobre o corpo B.
E) O trabalho realizado por sobre o corpo A é menor do que o trabalho realizado por sobre o corpo B.
Passo 1
Nessa questão vamos analisar o trabalho da força de atrito que, como realiza trabalho negativo, correspondente à dissipação de energia mecânica
Sabemos da relação entre a força de atrito, a força normal e o coeficiente de atrito cinético:
Decompondo a força normal, conforme a figura abaixo chegamos a:
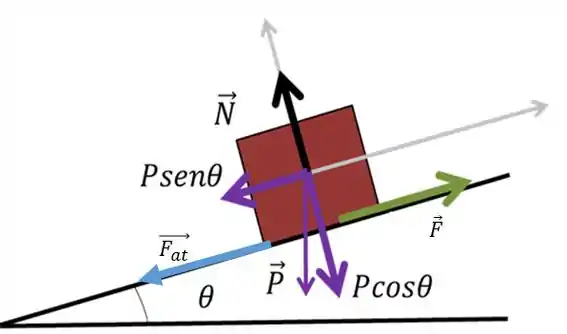
Então
E o trabalho do atrito =
Passo 2
Agora que vimos o conceito por trás do problema, vamos calcular o trabalho de atrito para cada massa e, assim, entender o quanto de energia é dissipada por cada uma.
Vemos que no bloco B a energia dissipada é maior, o que mostra que teremos uma energia mecânica maior quando o bloco A chega no topo.
Passo 3
Agora precisamos destrinchar essa energia mecânica em energia cinética e energia potencial gravitacional:
Como , podemos perceber que e
Assim, se os dois tivessem a mesma energia mecânica no ponto do topo, a energia cinética de A seria maior do que a de B.
No entanto, já vimos que a energia mecânica total do bloco é maior do que a de B quando chega ao topo, ou seja, a energia cinética será maior também.
Assim, chegamos à conclusão que:
Repare também que as duas últimas afirmativas estão incorretas, pois o trabalho realizado pela força é igual a
Ou seja, independe da massa de cada bloco. Assim, ambos os trabalhos (bloco A e bloco B) são iguais.
Resposta
(A)