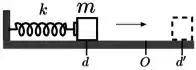
Um pequeno bloco de massa sobre uma mesa horizontal comprime uma mola de constante elástica de uma distância , a partir da posição relaxada da mola em , como mostra a figura. Liberado a partir do repouso, ele realiza um movimento retilíneo horizontal para a direita, onde ele perde o contato com a mola depois da posição , percorrendo em seguida uma distância , quando atinge o repouso; há uma força de atrito constante da supercifie da mesa sobre o bloco em toda a extensão do movimento. O coeficiente de atrito cinético entre a superfície e o bloco é:

Vamos começar escrevendo os dados do problema

Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.

No enunciado ele pede o coeficiente de atrito cinético, que é o coeficiente quando ele está se movendo. Nesse problema temos uma força dissipativa atuando, que é a força de atrito. Então

Onde é a energia mecânica em e é a energia mecânica em .

Precisamos achar , é e .

Começando por

O sinal do trabalho é negativo porque a força de atrito é no sentido contrário do movimento.

Já vimos em muitos outros exercícios que, no caso do bloco no plano

Então

Vamos agora achar as energias mecânicas. Em ambos os pontos não temos velocidade nem mudança de altura. A única energia é a potencial elástica, que está presente apenas no inicio.

Como ele perde contato com a mola no ponto ele não tem energia elástica

Lembrando rapidinho