Um carrinho de montanha russa se move sem atrito no trilho da figura abaixo. Ele sai do repouso do ponto A, situado a 40 metros do chão. Por questões de segurança, a força exercida no carrinho pelo trilho no ponto B não pode ser maior que 5 vezes o peso do carrinho.
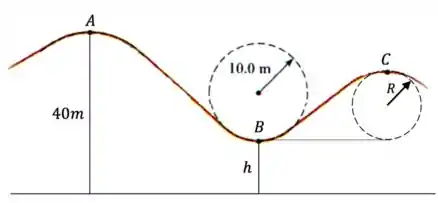
a) Considerando que no ponto A o carrinho descreve um círculo de raio 10 metros, qual deve ser a altura mínima ℎ para satisfazer o critério de segurança? Qual para essa altura mínima?
b) Considerando a altura mínima ℎ do item anterior, qual deve ser o raio mínimo R da curvatura no ponto C, que está a uma altura 2R acima de B, para que o carrinho não perca contato com o trilho quando passar por C? Qual para esse raio mínimo?
Passo 1
Oi oi galerinha, por aí tá tudo certo??
Vamos começar traduzinho esse enunciado aí hein! Vem comigoo!
a)
Vamos começar relembrando do Princípio de conservação de energia! Ou seja, incialmente nós tínhamos no ponto A uma energia potencial se transforma em energia cinética, logoooo, podemos considerar a igualdade seguinte.
Podemos substituir os valores dados no enunciado.
Passo 2
A ideia para desenrolar o próximo passo é usar a relação que o enunciado nos deu de que força exercida no carrinho pelo trilho no ponto B não pode ser maior que 5 vezes o peso do carrinho!
Sabendo que a força centrípeta é a responsável por manter a trajetória circular do corpo e pode ser calculada pela seguinte equação:
No ponto B, o peso do carrinho aponta para baixo e a normal para cima, logo:
Sabendo que a força exercida no carrinho pelo trilho no ponto B não pode ser maior que 5 vezes o peso do carrinho, então :
Logo:
Substituindo os valores que o nosso enunciado nos deu:
Então, para descobrirmos a altura , vamos substituir o valor de na equação (1).
Passo 3
Aqui no item b) nós vamos usar um raciocínio bem semelhante ao item a), o enunciado nos pergunta qual a altura no ponto C, em relação à altura em B, para que o carrinho não perca contato com o trilho.
Vamos começar associando que a altura em C equivale à .
Aqui nós também temos que considerar o princípio da conservação e energia, então é verdadeira a igualdade de que:
Travamos aqui, mas não precisa se desesperar, o macete é lembrar que para que o carrinho não saia dos trilhos, ele deve respeitar a igualdade de que a força centrípeta é igual a força peso!!
Logo,
Substituindo na equação (2), temos:
Como já temos o raio em C, podemos substituí-lo na equação da velocidade e determinamos , olha só!
Prontinhooo! Encontramos tudo que o enunciado nos pediu, ufa!