Um bloco de massa está comprimindo em uma mola ideal de constante elástica . Ao ser liberado do repouso, o bloco se desprende da mola percorrendo um piso horizontal sem atrito, quando então passa a um trecho horizontal de comprimento que oferece atrito de coeficiente cinético igual a . O bloco tem à sua frente uma rampa lisa, na qual ele para momentaneamente a uma altura máxima, tornando a descer a rampa, a passar novamente pelo trecho com atrito, a comprimir a mola e assim sucessivamente, até parar definitivamente. Adote

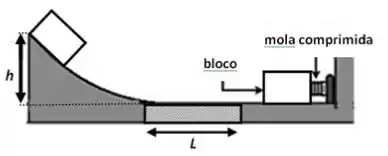
Determine:

(a) a variação de energia térmica do sistema bloco-piso na primeira vez que o bloco percorre completamente o trecho ;

(b) a maior altura que o bloco atinge na rampa;

(c) a compressão máxima da mola na primeira vez que o bloco retorna comprimindo-a;

d) a posição onde o bloco para definitivamente.

a)

Na letra a ele pede a variação de energia térmica. Bom, como vimos, nessa parte há dissipação de energia mecânica, que se dá em forma de energia térmica.

Então, equacionando isso, temos:

é a energia que a força de atrito está roubando do sistema. Essa força atua e um comprimento .

Então

Tem esse menos ali porque a força é contra o deslocamento, belê?

Portanto

b)A maior altura vai ser na primeira subida, pois é a maior energia que ele vai ter.

Vamos por partes. Não podemos conservar energia desde o ponto da mola até o de altura máxima, porque no meio do caminho tem atrito e a energia é dissipada. Então na primeira etapa, que é o trecho horizontal sem atrito, podemos ter conservação de energia:

Ele parte de repouso e após de soltar da mola ela fica relaxada, então

Já passei tudo para o SI, ok?

Então a energia com que o bloco chega na parte com atrito é

Agora, já vimos que nessa parte há uma dissipação de energia de Então após passar por essa etapa, a energia do bloco será

Beleza!

Agora ele vai começar a subir a rampa, que não tem atrito, então a energia mecânica se conserva. Como queremos saber a altura máxima, temos que nesse ponto a velocidade será momentaneamente nula. então

c) Então o bloco subiu e chegou nessa altura máxima. Agora ele vai descer, e quando chegar na região com atrito ele vai dissipar de energia de novo. E aí vai sair da região om atrito e vai comprimir a mola de novo.

Por partes. Primeiro, a energia que ele tinha na altura máxima é a mesma que ele vai ter quando chegar na parte com atrito. E depois quando passar vai ter dissipado

Aí ele passou e dissipou energia, então do outro lado da região com atrito a energia será:

Agora ele vai comprimir a mola, até parar, e nessa etapa, a energia se conserva.

d)

agora, vimos que a energia com que o boco deixa a mola nessa segunda vez:

Mas quando o bloco passar pela parte com atrito novamente vai ter dissipação de energia de . Então, assim que o bloco percorrer o comprimento de ele vai ficar com energia nula e vai parar. Então ele para na base da rampa.